Many months ago, I found a very interesting group theory problem (the if-part of the Proposition below) in Lee Zhuo Zhao‘s  -signature on Facebook. My first pathetic attempts to solve that problem failed, apparently it required deeper knowledge of group theory than I had at that time. But even after reading some introductory lecture notes on that topic, it took me ages until I succeeded in solving this problem. It wasn’t too difficult then to see that the conclusion is also reversible.
-signature on Facebook. My first pathetic attempts to solve that problem failed, apparently it required deeper knowledge of group theory than I had at that time. But even after reading some introductory lecture notes on that topic, it took me ages until I succeeded in solving this problem. It wasn’t too difficult then to see that the conclusion is also reversible.
I will prove the following result:
Proposition. Let  be a positive integer. Then every finite group of order
be a positive integer. Then every finite group of order  is cyclic if and only if
is cyclic if and only if
where 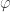 denotes the Euler’s Totient Function.
denotes the Euler’s Totient Function.
I will use the following notation: If  is a group and
is a group and 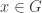 , then
, then 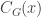 denotes the centraliser of
denotes the centraliser of  wrt to
wrt to  and
and  denotes the cyclic group generated by
denotes the cyclic group generated by  .
.
Proof of the if-part. Let  be a positive integer satisfying
be a positive integer satisfying  .
.
Note that using the canonical formula for 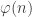 , it immediately follows that
, it immediately follows that  is squarefree.
is squarefree.
We will use induction on  . The claim is trivially true if
. The claim is trivially true if  is a prime number. Suppose now that for all positive integers
is a prime number. Suppose now that for all positive integers  with
with  , all groups of order
, all groups of order  are cyclic.
are cyclic.
Let  be a group of order
be a group of order  . We have to prove that
. We have to prove that  is cyclic. From the induction hypothesis and Lagrange’s theorem, it follows that all proper subgroups of
is cyclic. From the induction hypothesis and Lagrange’s theorem, it follows that all proper subgroups of  are cyclic.
are cyclic.
Lemma 1. Any two different elements of a cyclic subgroup of  are not conjugate.
are not conjugate.
Proof. Let  be a cyclic subgroup of
be a cyclic subgroup of  . Suppose that
. Suppose that  for integers
for integers  and some
and some 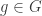 . We claim that
. We claim that  .
.
An immediate induction on  shows that
shows that
holds for all positive integers  . Putting
. Putting  , we see that
, we see that

,
so  divides
divides  . Clearly,
. Clearly,  and
and  divide
divide  . Furthermore,
. Furthermore,  is squarefree.
is squarefree.
Let  be a prime divisor of
be a prime divisor of  . Then
. Then  if and only if
if and only if  . If
. If  and
and  , then clearly
, then clearly  .
.
Otherwise, if 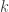 and
and  are not divisible by
are not divisible by  , then
, then  has a multiplicative inverse
has a multiplicative inverse  modulo
modulo  , so
, so  . Let
. Let  . Then
. Then  , so
, so  . Also,
. Also,  since
since  by Fermat’s little theorem. But
by Fermat’s little theorem. But  , so
, so  . It follows that
. It follows that  is a common divisor of
is a common divisor of  and
and 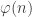 , so
, so  . Hence,
. Hence,  , so
, so  .
.
Thus, we see that  for all prime divisors
for all prime divisors  of
of  and since
and since  is squarefree, it follows that
is squarefree, it follows that  . But then
. But then  , as required.
, as required.
Next, we prove that the center of  is not trivial. Hence, assume for the sake of contradiction that the center
is not trivial. Hence, assume for the sake of contradiction that the center  of
of  is trivial.
is trivial.
Then for each 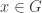 with
with  ,
, 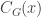 is a proper subgroup of
is a proper subgroup of  . Furthermore, this subgroup is maximal, for if
. Furthermore, this subgroup is maximal, for if  is a maximal proper subgroup containing
is a maximal proper subgroup containing  (we can assume it to be cyclic by the induction hypothesis), then
(we can assume it to be cyclic by the induction hypothesis), then  , so
, so  .
.
It follows that
Lemma 2. For each 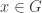 with
with  ,
, 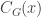 is the unique maximal proper subgroup of
is the unique maximal proper subgroup of  containing
containing  .
.
It is well known that if  is a cylic group of order
is a cylic group of order  and
and  is a divisor of
is a divisor of  then
then  contains a unique subgroup of order
contains a unique subgroup of order  , namely
, namely  .
.
Lemma 3. Let  and
and  be two maximal proper subgroups of
be two maximal proper subgroups of  and let
and let  and
and  . Suppose that
. Suppose that  . Then
. Then  and
and  are conjugate. In particular,
are conjugate. In particular,  .
.
Proof. Let  be a common prime divisor of
be a common prime divisor of 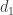 and
and  . Then
. Then  and
and  both contain a unique subgroup
both contain a unique subgroup  and
and  of order
of order  respectively. It follows from Lemma 2 that
respectively. It follows from Lemma 2 that  and
and  .
.
Furthermore, it follows from Sylow’s second theorem that  and
and  are conjugate, so
are conjugate, so  for some
for some 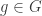 . Thus,
. Thus,  is a generator of
is a generator of  , wlog assume that
, wlog assume that  . Now,
. Now,

.
It follows that  , so
, so  .
.
Now, since the center of  is trivial, follows from the class equation that
is trivial, follows from the class equation that

, (1)
where 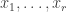 are representatives of the different nontrivial conjugacy classes. Each of the
are representatives of the different nontrivial conjugacy classes. Each of the  are maximal proper subgroups, the order of each two of them being either equal or coprime (Lemma 3). Furthermore, it is clear that for every prime divisor
are maximal proper subgroups, the order of each two of them being either equal or coprime (Lemma 3). Furthermore, it is clear that for every prime divisor  of
of  , there exists an
, there exists an  so that
so that  divides
divides  . Hence, we can write
. Hence, we can write  as
as  , where each of the
, where each of the 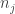 is the order of some of the
is the order of some of the  . Notice that
. Notice that 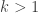 and
and  for all
for all  . Every summand in (1) is of the form
. Every summand in (1) is of the form  for some
for some  . Furthermore, for each
. Furthermore, for each  , each of the elements of
, each of the elements of  belong to different conjugacy classes by Lemma 1. Moreover, for each
belong to different conjugacy classes by Lemma 1. Moreover, for each  with
with  , we have that
, we have that  since
since  is a maximal proper subgroup of
is a maximal proper subgroup of  containing
containing  , which is unique by Lemma 2. It follows that in the sum in (1), the summand
, which is unique by Lemma 2. It follows that in the sum in (1), the summand  appears at least
appears at least  times for all
times for all  . Hence,
. Hence,
so
Thus,
and since  for all
for all  ,
,
so  , which is the desired contradiction.
, which is the desired contradiction.
It thus follows that the center  of
of  is not trivial. Let
is not trivial. Let  and
and  . Then
. Then  and
and  , so by the induction hypothesis, both
, so by the induction hypothesis, both  and
and  are cyclic. Let
are cyclic. Let 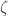 be a generator of
be a generator of  and
and  be a generator of
be a generator of  . Let
. Let  . Then
. Then  , so
, so  . Let
. Let  . Then
. Then  .
.
Assume that  . Then
. Then  divides
divides  for some prime divisor
for some prime divisor  of
of  . Since
. Since  ,
,
But  and
and  is squarefree, so
is squarefree, so  is divisible by exactly one of the numbers
is divisible by exactly one of the numbers  and
and  . But then, either
. But then, either

or

which is a contradiction. Hence  , so
, so  is cyclic, as required.
is cyclic, as required.
Proof of the only if-part. Let  be a positive integer satisfying
be a positive integer satisfying  . We have to show that there exists a finite group
. We have to show that there exists a finite group  of order
of order  that is not cyclic. The result is obvious if
that is not cyclic. The result is obvious if  is not squarefree, because if
is not squarefree, because if  is a multiple prime divisor of
is a multiple prime divisor of  , then the group
, then the group  is not cyclic.
is not cyclic.
Suppose now that  is squarefree and
is squarefree and  . Then there exist prime divisors
. Then there exist prime divisors  and
and  of
of  so that
so that 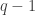 is divisible by
is divisible by  .
.
Let  be a primitive root modulo
be a primitive root modulo  . We consider the set
. We consider the set
Clearly,  since
since  for all
for all  if and only if
if and only if  and
and  .
.
Furthermore,  is a subgroup of the symmetric group
is a subgroup of the symmetric group  (the subgroup conditions can readily be verified). Let
(the subgroup conditions can readily be verified). Let  send
send  to
to 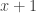 and
and  send
send  to
to  . Then
. Then  sends
sends  to
to  and
and  sends
sends  to
to  , so
, so  is not abelian.
is not abelian.
Consider now the group  . Since
. Since  ,
,  . But
. But  is not abelian, so
is not abelian, so  is not abelian. In particular,
is not abelian. In particular,  is not cyclic. This completes the proof.
is not cyclic. This completes the proof.
Remark. For 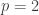 , the group
, the group  constructed in the proof of the “only if”-part above is isomorphic to the dihedral group
constructed in the proof of the “only if”-part above is isomorphic to the dihedral group  of a regular
of a regular  -gon.
-gon.
Further Remark. I have just noticed that the group  is acutally isomorphic to the semidirect product
is acutally isomorphic to the semidirect product  wrt to the homomorphism
wrt to the homomorphism

,

.
, where
is a finite set of vertices,
is a finite set of weights and
is a partial map. An automorphism of
is a bijection
such that for all
,
is defined if and only if
is defined in which case
. The group of all automorphisms of
is denoted by
. If
, then
denotes the (total) degree of
.
be a weighted directed graph with
for all
. Then there exists a simple graph
with
.
for some
. Construct
from
by replacing every edge
with
by

induces an automorphism of
in the canonical way while it is easy to see that every automorphism of
must necessarily permute the original vertices and thus be equal to one of the induced automorphisms.
be an arbitrary finite group with order at least three (the other cases are trivial). Construct a weighted directed graph by putting
and
for all
, and for
, let
. Note that
is an automorphism of the graph for all
since
and that
.
is an automorphism of the graph, let
and
be arbitrary. Then
, so
, i.e.
. It follows that
and by the lemma above, there exists also a simple graph with automorphism group
.
