A major research interest of mine is the investigation of EKR problems in different settings. This type of results is named after the well-known seminal result by Erdős, Ko and Rado on uniform set systems.
Theorem Let  and
and  be a set of
be a set of  -sets of an
-sets of an  -element ground set such that no two are disjoint. Then
-element ground set such that no two are disjoint. Then  and the only examples attaining equality are the point-pencils (i.e. all
and the only examples attaining equality are the point-pencils (i.e. all  -sets through a fixed point).
-sets through a fixed point).
There are plenty of similar theorems in different contexts, where the “no two disjoint” property is replaced by an appropriate notion of “no two far apart”. An almost unreasonably successful technique in this setting (there’s a whole book about it!) is to rephrase the problem in terms of finding the largest coclique in a certain graph and applying the ratio bound. Very often, this will already provide a sharp upper bound.
Theorem (the ratio bound, often attributed to Hoffman and Delsarte).
Let

be a

-regular graph on

vertices and

be the smallest eigenvalue of its adjacency matrix. Then
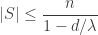 .
.
If equality is attained, then the characteristic vector of

lies in

, where
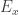
denotes the eigenspace corresponding to the eigenvalue

(of the adjacency matrix of

).
For example: in the setting of the original EKR result, we construct a graph with vertex set all  -sets of the
-sets of the  -set, making two
-set, making two  -sets adjacent whenever they are disjoint. This graph is commonly known as the Kneser graph. It is a regular graph on
-sets adjacent whenever they are disjoint. This graph is commonly known as the Kneser graph. It is a regular graph on 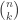 vertices of valency
vertices of valency 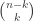 . One can show that the smallest eigenvalue is
. One can show that the smallest eigenvalue is  (we will not prove this). After a small computation, one immediately deduces the bound in the EKR theorem.
(we will not prove this). After a small computation, one immediately deduces the bound in the EKR theorem.
After obtaining an upper bound, the next step would be to classify the maximal examples, which is made possible by the extra information the ratio bound provides. In order to classify maximal examples, it thus makes sense to search for a good description of these eigenspaces.
Sam Adriaensen, my colleague at VUB, told me about a nice technique he used (in work in progress) to find a basis for these eigenspaces. Incidentally, this same technique in a paper by Fallat, Meagher and Shirazi, which he apparently was unaware of! Most likely the idea was already known even earlier, but as it was new to me, I decided to record it here.
The main idea is to use the notion of quotient matrices. This object is already explained in detail in the preprint by Fallat, Meagher and Shirazi mentioned before, but let’s recall its main properties. Suppose you have  -regular graph
-regular graph  with vertex set
with vertex set 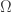 . Consider a partition
. Consider a partition  such that every induced subgraph on
such that every induced subgraph on  ,
,  is a biregular graph and the induced subgraph on every
is a biregular graph and the induced subgraph on every  is regular. Such a partition is called an equitable partitition.
is regular. Such a partition is called an equitable partitition.
Equitable partitions are easily found: consider the partition in orbits by any subgroup of the automorphism group of  .
.
Definition The quotient matrix of the equitable partition 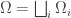 is the
is the  matrix
matrix 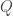 , where
, where  is the number of neighbours in
is the number of neighbours in  a vertex in
a vertex in  has.
has.
The key fact is that the eigenvalues of 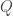 are also eigenvalues of the adjacency matrix of
are also eigenvalues of the adjacency matrix of  which follows from the fact that eigenvectors can be “blown up”: if
which follows from the fact that eigenvectors can be “blown up”: if  is an eigenvector of
is an eigenvector of 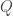 with eigenvalue
with eigenvalue  , then define the vector
, then define the vector  by setting
by setting  , whenever
, whenever 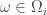 . This vector will also be an eigenvector of the adjacency matrix of
. This vector will also be an eigenvector of the adjacency matrix of  (this is a matter of computation).
(this is a matter of computation).
In the example of the Kneser graph, we can partition its vertex set depending on whether the corresponding  -set contains a fixed element form the
-set contains a fixed element form the  -set or not. The quotient matrix has the form
-set or not. The quotient matrix has the form
 .
.
The eigenvalues of 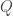 are
are 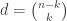 , and
, and  , which we recall is the smallest eigenvalue! Their multiplicities as eigenvalues of
, which we recall is the smallest eigenvalue! Their multiplicities as eigenvalues of  are
are  and
and 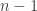 (a fact which we will again not prove). Here comes the essence of the technique: since
(a fact which we will again not prove). Here comes the essence of the technique: since 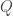 is invertible, the vector
is invertible, the vector 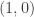 is in its rowspace and is hence a lineair combination of eigenvectors corresponding to
is in its rowspace and is hence a lineair combination of eigenvectors corresponding to  and
and  . Since we can “blow up” these vectors, this means that the characteristic vector of the family
. Since we can “blow up” these vectors, this means that the characteristic vector of the family  of all sets through the fixed point is also a vector that lies
of all sets through the fixed point is also a vector that lies  !
!
Varying the point, we find a set of  vectors in
vectors in 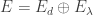 , and it is not too hard to show that they are in fact linearly independent and hence form a basis of
, and it is not too hard to show that they are in fact linearly independent and hence form a basis of  . In other words, (the characteristic vectors of) the point-pencils are a basis of this space. From here on out, it is again not too difficult (see the Godsil-Meagher book p.123 for the details) to show that there are no other maximal intersecting families in this eigenspace, from which the classification follows.
. In other words, (the characteristic vectors of) the point-pencils are a basis of this space. From here on out, it is again not too difficult (see the Godsil-Meagher book p.123 for the details) to show that there are no other maximal intersecting families in this eigenspace, from which the classification follows.
The crux of the argument is a neat little observation, yet non-trivial facts result from it. I have been able to apply the idea of using quotient matrices in order to find eigenvectors of large matrices myself recently in a slightly different way, with the same motivation. The situation is a bit trickier, so it remains to be seen whether we will fully succeed. Hopefully I will be able to share this soon!
on the arXiv. This work is a natural successor of earlier results by Philipp, Klaus and Jesse Lansdown for type
(see later).
in the majority of cases must be blow-ups from ‘trivial’ sets of collinear points or intersecting generators. I was quite optimistic at the start of this project that the techniques from Philipp and Klaus’ earlier work on type
could be readily extended to type
, even stating to Philipp at some point in June last year ‘it could be done over the summer’. Turns out it wasn’t so easy after all.


