Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
| CARVIEW |
Select Language
HTTP/2 200
date: Sun, 18 Jan 2026 19:42:59 GMT
server: Apache
set-cookie: WR_SID=6e088356.648aec82dda49; path=/; expires=Wed, 16-Jan-36 19:43:00 GMT; domain=.wolfram.com
strict-transport-security: max-age=2592000;
strict-transport-security: max-age=2592000;
vary: Origin,Accept-Encoding
content-security-policy: default-src * wolfram+cloudobject: data: 'unsafe-eval' 'unsafe-inline'; img-src * blob: data:;
cache-control: public, max-age=60
x-generatedfrom: Generated from the Wolfram Cloud: https://www.wolfram.com/cloud
x-terms-of-use: Terms of use: https://www.wolfram.com/legal/terms/wolfram-cloud.html
x-data-source-information: Data source information: https://wolfram.com/knowledgebase/source-information
x-content-type-options: nosniff
x-xss-protection: 1; mode=block
content-type: text/html;charset=utf-8
content-encoding: gzip
content-length: 12429
set-cookie: WR_SID=70cb5cbe.648aec82df294; path=/; max-age=315360000; domain=.wolframcloud.com
set-cookie: JSESSIONID=0F91EABC008C48E98F51164B78964AD9; Domain=wolframcloud.com; Path=/; HttpOnly
ExtendedLatticeReduce | Wolfram Function Repository
Extended
Function Repository Resource:
Extended
Compute a reduced basis for a set of vectors, along with a unimodular matrix that converts from the vectors to the reduced basis
Contributed by:
Daniel Lichtblau
ResourceFunction["ExtendedLatticeReduce"][lat] computes a reduced basis ℬ for the lattice of integer vectors lat, returning the pair {𝒰,ℬ}, where 𝒰 is a unimodular conversion matrix satisfying 𝒰.lat=ℬ. |
Details and Options
The input lattice lat must be a matrix of integers and/or rational numbers. Gaussian integers and rationals are also permitted.
The conversion matrix is square and unimodular (it has determinant equal to ±1).
ResourceFunction["ExtendedLatticeReduce"][lat,"ReductionLambda"→λ] will use the value λ for the reduction ratio in the LLL algorithm.
The reduction ratio λ must be in the range 1/4 ≤ λ<1.
The value of the "ReductionLambda" option setting can affect the speed and quality of the reduction. A lower value will typically give a faster computation, but result in a lattice that is further from being fully reduced (it will of course be reduced in the LLL sense appropriate for the parameter setting).
Examples
Basic Examples (5)
Create an integer lattice comprised of two columns of large integers augmented on the right by an identity matrix:
| In[1]:= |
![SeedRandom[1234];
lat = Join[RandomInteger[{-10^8, 10^8}, {4, 2}], IdentityMatrix[4], 2]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/0fdd0a331be1e6c8.png){kind=small}
|
| Out[1]= |
|
Reduce the lattice:
| In[2]:= |
![{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/1f62493793c374a0.png){kind=small}
|
| Out[2]= |
|
Check the conversion matrix equation:
| In[3]:= |
|
| Out[3]= |
|
Check that the conversion matrix is unimodular:
| In[4]:= |
![Det[umat]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/0607c461b01aa7fa.png){kind=small}
|
| Out[4]= |
|
Check that LatticeReduce gives the same reduced lattice (this is not strictly necessary):
| In[5]:= |
![LatticeReduce[lat]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/393b9ef1352d36d4.png){kind=small}
|
| Out[5]= |
|
Scope (2)
Create a rational lattice:
| In[6]:= |
![SeedRandom[1234];
lat = RandomInteger[{-10^8, 10^8}, {4, 5}]/
RandomInteger[{1, 10^3}, {4, 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/6f9f544ae30888c2.png){kind=small}
|
| Out[6]= |
|
Compute a reduction of the lattice along with the corresponding unimodular conversion matrix::
| In[7]:= |
![{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/72752812ab5abf3a.png){kind=small}
|
| Out[7]= |
|
Reduce a lattice of Gaussian integers with larger entries in the leftmost two columns:
| In[8]:= |
![SeedRandom[1234];
c1 = 2;
c2 = 5;
lat = Join[
RandomInteger[{-10^8, 10^8}, {4, c1}] + I*RandomInteger[{-10^8, 10^8}, {4, c1}], RandomInteger[{-10^3, 10^3}, {4, c2}] + I*RandomInteger[{-10^3, 10^3}, {4, c2}], 2];
{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/1f1aad256e749167.png)
|
| Out[8]= |
|
Check the result:
| In[9]:= |
![{Det[umat], Max[Abs[umat . lat - redlat]]}](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/5de612ddf5066398.png){kind=small}
|
| Out[9]= |
|
Options (7)
ReductionLambda (7)
Create a large matrix with big integers in the first two columns and an identity matrix on the right:
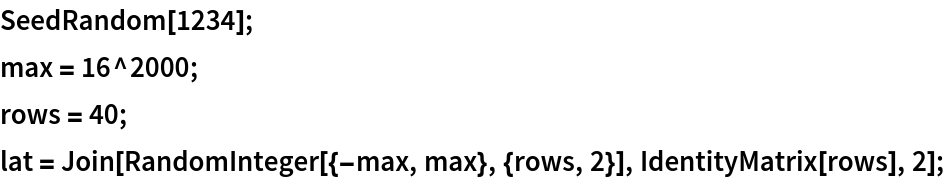
First compute the default reduction:
| In[10]:= |
![Timing[{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat];]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/5983c06041f161b6.png){kind=small}
|
| Out[10]= |
|
Check the conversion matrix criteria:
| In[11]:= |
![{Abs[Det[umat]] == 1, Max[Abs[umat . lat - redlat]] == 0}](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/1ad08264ecaca651.png){kind=small}
|
| Out[11]= |
|
Computing a reduction of higher quality typically takes longer:
| In[12]:= |
![Timing[{umat2, redlat2} = ResourceFunction["ExtendedLatticeReduce"][lat, "ReductionLambda" -> 0.999];]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/2b58d96a32020358.png){kind=small}
|
| Out[12]= |
|
Using a smaller reduction size ratio setting typically gives a faster computation:
| In[13]:= |
![Timing[{umat3, redlat3} = ResourceFunction["ExtendedLatticeReduce"][lat, "ReductionLambda" -> 1/4];]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/7c9fa31cd16a968b.png){kind=small}
|
| Out[13]= |
|
The higher quality reduction manifests by most rows in the “stronger” result having norms smaller than for corresponding rows in the default reduction:
| In[14]:= |
![Map[Norm[N[#]] &, redlat2]/Map[Norm[N[#]] &, redlat]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/3bc0d9162e65008c.png){kind=small}
|
| Out[14]= |
|
The lower quality reduction manifests by most rows in the “weaker” result having norms larger than for corresponding rows in the default reduction:
| In[15]:= |
![Map[Norm[N[#]] &, redlat3]/Map[Norm[N[#]] &, redlat]](https://www.wolframcloud.com/obj/resourcesystem/images/8a3/8a36cdcf-baa5-4769-af66-0c8877992651/1d364302f62f73b6.png){kind=small}
|
| Out[15]= |
|
Related Links
Version History
- 2.0.0 – 26 May 2021
- 1.0.0 – 07 October 2019
Source Metadata
- Citation:
- Andrew Novocin, Damien Stehlé. An LLL-Reduction Algorithm with Quasi-linear Time Complexity. STOC ‘11: Proceedings of the forty-third annual ACM symposium on Theory of computing, June 2011 Pages 403–412.
https://doi.org/10.1145/1993636.1993691
Related Resources
Related Symbols
Author Notes
A different implementation of this functionality, written by Wilberd van der Kallen, is available at the Wolfram Library Archive link provided.
Version 2 uses a "sometimes asymptotically fast" divide-and-conquer algorithm similar to that used in the half-GCD algorithm for integer GCD computations. This is done whenever the input lattice consists of integers or Gaussian integers and has full row rank. A more rigorous version is informally referred to as L1Plus. The theory behind it is in the links. This implementation qualities as "quick and dirty" and does not come with any guarantee about asymptotic speed other than it promises to try hard and do the best it can.
License Information
This work is licensed under a Creative Commons Attribution 4.0 International License