Happy new year to everyone who is still following this blog! For this new post (coming after a nontrivial break), I thought I should perhaps try something different, and so I decided that it might be a good idea to discuss an open problem which I like, and which has been on the back of my mind lately.
Long story short, it’s a problem that Oleksiy Klurman and I came up with together a few years ago, and which we excitedly shared with some of our friends at various workshops and conferences, but we never really got a chance to write it down anywhere (mostly because we couldn’t prove anything particularly interesting about it..). In the meantime, one of us started a blog, so we thought the other day that we might finally have an opportunity to say some things about this problem in a sufficiently formal way and perhaps voice some of our frustrations.
To put this into context, let me start by introducing some notation and discussing some classical results about Sidon sets. For a set of real numbers  , let
, let  denote the size of the largest subset
denote the size of the largest subset  of
of  with the property that there are no nontrivial solutions to the equation
with the property that there are no nontrivial solutions to the equation  , where
, where  are pairwise distinct from each other. Such a set
are pairwise distinct from each other. Such a set  is called an additive Sidon subset of
is called an additive Sidon subset of  , so
, so  thus denotes the size of the largest additive Sidon subset of
thus denotes the size of the largest additive Sidon subset of  . One of the most classical problems in additive combinatorics is to determine
. One of the most classical problems in additive combinatorics is to determine 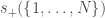 for sufficiently large positive integers
for sufficiently large positive integers  . For brevity, we will denote this function in this case by
. For brevity, we will denote this function in this case by  .
.
Let’s discuss a few things about this  . First, since all the pairwise sums live in the interval
. First, since all the pairwise sums live in the interval  , it is easy to see that
, it is easy to see that  , which implies that
, which implies that  . In 1941, Erdos and Turan refined this simple observation and proved that
. In 1941, Erdos and Turan refined this simple observation and proved that  . This was further sharpened by Lindstrom, who established the inequality
. This was further sharpened by Lindstrom, who established the inequality

which is the best known upper bound for  . In order to produce a good lower bound for
. In order to produce a good lower bound for  , one needs to construct a large subset of
, one needs to construct a large subset of  with all of its two element subset sums distinct. In their paper already cited above, Erdos and Turan proceeded as follows. Fix a prime
with all of its two element subset sums distinct. In their paper already cited above, Erdos and Turan proceeded as follows. Fix a prime 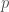 , and let
, and let 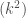 be the unique integer in
be the unique integer in  congruent to
congruent to  modulo
modulo 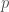 . It is not hard to check that
. It is not hard to check that 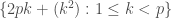 is a Sidon set contained in the interval
is a Sidon set contained in the interval  . In particular, for
. In particular, for  and
and 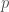 sufficiently large this construction already leads to the fact that
sufficiently large this construction already leads to the fact that

holds for all  sufficiently large. This is essentially a Freiman isomorphism from the
sufficiently large. This is essentially a Freiman isomorphism from the  parabola in
parabola in  . Three different constructions due to Singer, Bose, and Ruzsa, all with a similar algebraic flavor, lead to a slightly better lower bound for
. Three different constructions due to Singer, Bose, and Ruzsa, all with a similar algebraic flavor, lead to a slightly better lower bound for  than the one above, which is of the form
than the one above, which is of the form

While all of these results are quite classical, determining whether the correct size of  is closer to the upper bound or to the lower bound (i.e. if the lower order term in Lindstrom’s upper bound is required) and what all these extremal Sidon sets might look like are still major open problems. We refer the interested reader to this consult this nice survey of O’Bryant and this beautiful blog post of Gowers for more information.
is closer to the upper bound or to the lower bound (i.e. if the lower order term in Lindstrom’s upper bound is required) and what all these extremal Sidon sets might look like are still major open problems. We refer the interested reader to this consult this nice survey of O’Bryant and this beautiful blog post of Gowers for more information.
Similarly, one can play the same game with multiplication. For a set of real numbers  , let us now define
, let us now define  to be the size of the largest subset
to be the size of the largest subset  of
of  with the property that there are no nontrivial solutions to the equation
with the property that there are no nontrivial solutions to the equation 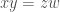 , where
, where  are pairwise distinct from each other. Naturally, we will call
are pairwise distinct from each other. Naturally, we will call  a multiplicative Sidon subset of
a multiplicative Sidon subset of  , so like before
, so like before  simply stands for the size of the largest multiplicative Sidon subset of
simply stands for the size of the largest multiplicative Sidon subset of  .
.
When  , the story of
, the story of  turns out to be a bit more pleasant than the story of
turns out to be a bit more pleasant than the story of  . At first glance, this is perhaps not too surprising. First of all, it is easy to see that
. At first glance, this is perhaps not too surprising. First of all, it is easy to see that  is much larger than
is much larger than  . For example, one can consider
. For example, one can consider  to be the set of prime numbers inside the interval
to be the set of prime numbers inside the interval  . This is a multiplicative Sidon set and, by the Prime number theorem,
. This is a multiplicative Sidon set and, by the Prime number theorem,  ; therefore, we know that
; therefore, we know that  , which is somewhat promising. Indeed, in 1938 (three years before his additive Sidon paper with Turan), Erdos had in fact already started the study this quantity and managed to further improve upon this simple construction by showing that
, which is somewhat promising. Indeed, in 1938 (three years before his additive Sidon paper with Turan), Erdos had in fact already started the study this quantity and managed to further improve upon this simple construction by showing that

for some absolute constant  , where
, where  stands as usual for the number of primes in
stands as usual for the number of primes in  . Moreover, in the same paper he also proved that
. Moreover, in the same paper he also proved that  , upper bound which 31 years later he himself refined to
, upper bound which 31 years later he himself refined to  , thus establishing the correct order of magnitude of the lower order term, namely
, thus establishing the correct order of magnitude of the lower order term, namely

So, to (abruptly) summarize: while for  we are still fairly troubled regarding the correct order of magnitude and the nature of the largest additive Sidon subsets in
we are still fairly troubled regarding the correct order of magnitude and the nature of the largest additive Sidon subsets in  , for the multiplicative Sidon story we know quite well what
, for the multiplicative Sidon story we know quite well what  is, and we also know that these extremal sets are intimately connected with the primes.
is, and we also know that these extremal sets are intimately connected with the primes.
But what do we know about  and
and  for other sets of reals
for other sets of reals  ? When
? When  is multiplicatively structured, say
is multiplicatively structured, say 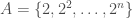 , we have that
, we have that  and
and  , so the roles are in some sense reversed. Needless to say, this situation resembles quite well the dichotomy that motivated the celebrated sum-product conjecture of Erdos and Szemeredi, which roughly states that no set has a polynomial saving for both the size of the sum set and the size of the product set, over the trivial quadratic upper bound. So perhaps, one can formulate an analogous conjecture.. (and, of course, that’s what we did!).
, so the roles are in some sense reversed. Needless to say, this situation resembles quite well the dichotomy that motivated the celebrated sum-product conjecture of Erdos and Szemeredi, which roughly states that no set has a polynomial saving for both the size of the sum set and the size of the product set, over the trivial quadratic upper bound. So perhaps, one can formulate an analogous conjecture.. (and, of course, that’s what we did!).
Question. (KP) For every set of reals  , is there an absolute constant
, is there an absolute constant 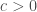 such that
such that
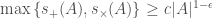
for every 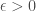 ?
?
It is perhaps important to mention that we couldn’t find this anywhere in the literature, but that we did not look terribly hard for a reference (as I said, we more or less just asked around!). So, not only that we’d be (very) excited if someone can solve it, but we’d also be quite grateful if anyone knows a reference where something along these lines has been already asked.
In the remaining time/space, I’d like to draw attention towards a particularly tantalizing special case, which seems already quite tricky. Suppose  is a set of reals with small doubling, namely
is a set of reals with small doubling, namely  , where
, where 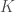 may possibly depend on
may possibly depend on  . We know that there are such sets with
. We know that there are such sets with  , so the question here is: can one prove that we always have
, so the question here is: can one prove that we always have  for every
for every 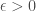 ?
?
By using Solymosi’s theorem that every set  satisfies
satisfies 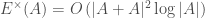 , where
, where  stands for the number quadruples
stands for the number quadruples  with
with  and
and  ,
,  ,
,  ,
,  pairwise distinct, it is not difficult to prove that every set
pairwise distinct, it is not difficult to prove that every set  with
with  contains a multiplicative Sidon subset of size
contains a multiplicative Sidon subset of size 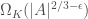 for every
for every 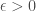 . Indeed, one can take a random subset
. Indeed, one can take a random subset 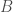 of
of  , obtained by choosing each element of
, obtained by choosing each element of  to be part of
to be part of 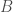 with probability
with probability ![p \in [0,1]](https://s0.wp.com/latex.php?latex=p+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=404040&s=0&c=20201002) independently, and then removing one element from each multiplicative quadruple in
independently, and then removing one element from each multiplicative quadruple in 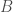 . The end result is some smaller (random) set
. The end result is some smaller (random) set 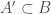 with no multiplicative quadruples, which on average will have size
with no multiplicative quadruples, which on average will have size
![\mathbb{E}[|A'|] \geq p|A| - c p^{4} |A+A|^{2}\log |A|,](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5B%7CA%27%7C%5D+%5Cgeq+p%7CA%7C+-+c+p%5E%7B4%7D+%7CA%2BA%7C%5E%7B2%7D%5Clog+%7CA%7C%2C&bg=ffffff&fg=404040&s=0&c=20201002)
for some absolute constant 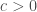 . Thus, there must exist a multiplicative Sidon subset of
. Thus, there must exist a multiplicative Sidon subset of  of at least that size. Using the fact that
of at least that size. Using the fact that  and optimizing for
and optimizing for 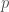 in terms of
in terms of  then proves the claim. And surprise, surprise, this is more or less the only nontrivial thing that we could say! We think that one can maybe hope to use ideas from the proof of Solymosi’s sum-product theorem more directly rather than the result itself as a blackbox in order to do better than
then proves the claim. And surprise, surprise, this is more or less the only nontrivial thing that we could say! We think that one can maybe hope to use ideas from the proof of Solymosi’s sum-product theorem more directly rather than the result itself as a blackbox in order to do better than  , but we couldn’t find any such argument. Even when
, but we couldn’t find any such argument. Even when 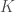 is small enough to allow the application of Freiman’s theorem, we didn’t know how to use the generalized arithmetic progression structure of
is small enough to allow the application of Freiman’s theorem, we didn’t know how to use the generalized arithmetic progression structure of  to do any better (except perhaps in some situations where one adds some further assumptions on
to do any better (except perhaps in some situations where one adds some further assumptions on  ). So, any ideas would be very welcome!
). So, any ideas would be very welcome!
That being said, I’d also like to add that a friendlier direction which seems to be still worth investigating is the “dual” regime where  , where
, where 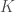 is an absolute positive constant. By the multiplicative variant of Freiman’s theorem,
is an absolute positive constant. By the multiplicative variant of Freiman’s theorem,  must in this case lie in a multiplicative subgroup of
must in this case lie in a multiplicative subgroup of  of small rank
of small rank  (bounded only in terms of
(bounded only in terms of 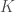 ), so by quantitative variants of Schmidt’s subspace theorem such as the one due to Amoroso and Viada it is also not too difficult to find “almost Sidon sets” of size
), so by quantitative variants of Schmidt’s subspace theorem such as the one due to Amoroso and Viada it is also not too difficult to find “almost Sidon sets” of size  . To be more precise, for every
. To be more precise, for every 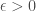 , there exists some positive integer
, there exists some positive integer  and a subset
and a subset  of
of  of size
of size  with the property that each sum of two distinct elements in
with the property that each sum of two distinct elements in  has multiplicity at most
has multiplicity at most 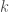 . This also follows from a probabilistic deletion argument in the style of the one above, although it is a bit more technical. Nevertheless, it seems likely that finite subsets of multiplicative subgroups of
. This also follows from a probabilistic deletion argument in the style of the one above, although it is a bit more technical. Nevertheless, it seems likely that finite subsets of multiplicative subgroups of  of small rank might actually have linear size additive Sidon subsets for some “easier” reasons (e.g. the primordial subset
of small rank might actually have linear size additive Sidon subsets for some “easier” reasons (e.g. the primordial subset  , which is contained in a rank
, which is contained in a rank 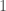 multiplicative subgroup, is Sidon itself due to the uniqueness of binary representations).
multiplicative subgroup, is Sidon itself due to the uniqueness of binary representations).
Later edit: In a comment, Oliver Roche-Newton already provided a simple construction which shows that answer to the original question cannot be yes as for any  : there exists a set
: there exists a set  with no additive/multiplicative Sidon subsets of size greater than
with no additive/multiplicative Sidon subsets of size greater than 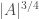 . This set however does not have small additive or multiplicative doubling, so the two particular cases described above could still be true. It also still remains to see whether there exists
. This set however does not have small additive or multiplicative doubling, so the two particular cases described above could still be true. It also still remains to see whether there exists  such that
such that

for some absolute constant  . This would already be quite interesting (and in the spirit of the sum-product theorem of Erdos and Szemeredi). That being said, it is perhaps also useful to add that
. This would already be quite interesting (and in the spirit of the sum-product theorem of Erdos and Szemeredi). That being said, it is perhaps also useful to add that

follows from a more general result of Komlos, Sulyok and Szemeredi which implies that 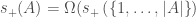 holds for all sets of integers
holds for all sets of integers  . It is not difficult to see that once we have this over the integers,
. It is not difficult to see that once we have this over the integers,  also holds for all sets of reals
also holds for all sets of reals  (by using a diophantine approximation argument, for example). Since
(by using a diophantine approximation argument, for example). Since 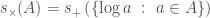 (ignoring small issues), this also implies
(ignoring small issues), this also implies  .
.
Later edit 2: In the meantime, I’ve also become aware of improved constructions by Oliver Roche-Newton+Audie Warren and (independently) Ben Green+Sarah Peluse which show that the original conjecture cannot be true as stated for any 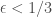 : there exists a set
: there exists a set  with no additive/multiplicative Sidon subsets of size greater than
with no additive/multiplicative Sidon subsets of size greater than  . Moreover, these constructions also have small additive doubling, so they also show the (rather curious) fact that the
. Moreover, these constructions also have small additive doubling, so they also show the (rather curious) fact that the 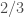 exponent obtained via probabilistic deletion and Solymosi’s theorem which I sketched (for the size of the largest multiplicative Sidon subset in
exponent obtained via probabilistic deletion and Solymosi’s theorem which I sketched (for the size of the largest multiplicative Sidon subset in  when
when  ) is actually sharp. More updates to come. (I hope!)
) is actually sharp. More updates to come. (I hope!)
-dimensional convex polytopes, go back to the antiquity, while others are motivated by connections with different areas of modern mathematics, in particular combinatorics, harmonic analysis, number theory, and topology. Every now and then, a new phenomenon is discovered in one place and this leads to surprising progress on all fronts. Over the past few years in particular, several breakthrough results have been discovered, answering or nearly answering some of the oldest problems in the field. In this REU project we will try to capitalize a little bit on this momentum. We will study some of these recent developments in the area (and some other remarkable developments from adjacent areas, e.g. extremal combinatorics), and then aim to make progress on a few new problems. Possible topics could include: incidence geometry, (hyper)graph theory, Ramsey theory, convex geometry, topological combinatorics, or coding theory.
