Anyone who has spent any amount of time in algebra or analysis has come across vector spaces: a set of elements, vectors, which we can add together or multiply by a scalar from some fixed field. This idea is simple and natural enough that students in high-school physics classes become familiar with the basic idea of vectors, if only in an informal way. However, in the axioms of a vector space there’s nothing that particularly requires that we pull our scalars from a field (though other results in vector space theory depend on our having an underlying field). Indeed, we could just require that the scalars we multiply by simply be elements of a ring; this gives us a structure known as a module. Though this seems like a simple enough generalization, module theory has some quirks that those of us more accustomed to vector spaces will find odd. For instance, though every vector space has a basis, there are modules which do not; and even if a module has a basis, two different bases may have different cardinalities.
To be more precise, given a ring  and an abelian group
and an abelian group  (written additively), we say that
(written additively), we say that  is a (left)
is a (left)  -module if there exists a ring homomorphism
-module if there exists a ring homomorphism  . (Recall that if
. (Recall that if  is an abelian group, the collection of endomorphisms of
is an abelian group, the collection of endomorphisms of  forms a ring under piecewise addition and function composition.) This says simply that given an
forms a ring under piecewise addition and function composition.) This says simply that given an 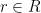 and an
and an 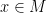 , we can define the multiplication of
, we can define the multiplication of  by
by  as
as  . Given any
. Given any  and any
and any  , the following are immediate consequences of our definition.
, the following are immediate consequences of our definition.
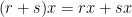

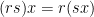
If in addition the ring  has an identity, we may also require that
has an identity, we may also require that  for all
for all 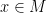 . We call such a module unitary. Though this isn’t strictly required, we will assume that all modules we deal with are unitary if the ring has identity. Notice that we only perform multiplication on the left. If we define multiplication on the right, we have a right
. We call such a module unitary. Though this isn’t strictly required, we will assume that all modules we deal with are unitary if the ring has identity. Notice that we only perform multiplication on the left. If we define multiplication on the right, we have a right  -module. We will assume that all of our modules are left module unless otherwise specified.
-module. We will assume that all of our modules are left module unless otherwise specified.
The three properties listed above aren’t simply consequences of our definition of a module, but can actually be used as an alternative definition. That is, if we have an abelian group  , a ring
, a ring  , and some multiplication
, and some multiplication  satisfying the above properties, we then have a module. To see this, define for each
satisfying the above properties, we then have a module. To see this, define for each 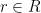 a
a  -endomorphism
-endomorphism 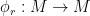 by
by  . Notice that the second property above guarantees that
. Notice that the second property above guarantees that  is indeed an endomorphism:
is indeed an endomorphism: 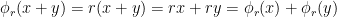 . Now defining a map
. Now defining a map  as
as  , properties one and three guarantee that this is in fact a ring homomorphism.
, properties one and three guarantee that this is in fact a ring homomorphism.
As stated earlier, a module can be thought of as a generalization of a vector space. In fact, if our ring  is a field, then any
is a field, then any  -module is simply a vector space over
-module is simply a vector space over  . A module can also be thought of as a generalization of an abelian group, in the sense that every abelian group is in fact a
. A module can also be thought of as a generalization of an abelian group, in the sense that every abelian group is in fact a 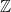 -module. Suppose that
-module. Suppose that  is an abelian group. For each positive
is an abelian group. For each positive  , define
, define 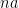 as
as  . If
. If  , define
, define  . Finally, if
. Finally, if  , define
, define 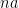 as the inverse (in
as the inverse (in  ) of
) of  .
.
Notice that every ring can be viewed as a module over itself;  is an
is an  -module where scalar multiplication is simply the ring’s usual multiplication. Additionally, if
-module where scalar multiplication is simply the ring’s usual multiplication. Additionally, if  is a subring of
is a subring of  , then
, then  can be viewed as an
can be viewed as an  -module as the three properties of an
-module as the three properties of an  -module are satisfied by usual multiplication in the ring. Similarly, if
-module are satisfied by usual multiplication in the ring. Similarly, if 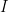 is left ideal of
is left ideal of  , then
, then 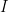 is a left
is a left  -module; if
-module; if 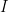 is a right ideal, then it’s a right
is a right ideal, then it’s a right  -module.
-module.
As we may pull our scalars from a ring instead of a field, we can treat some more “interesting” objects are scalars. For instance, suppose that 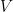 is an
is an 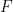 -vector space and
-vector space and  a linear transformation. Then
a linear transformation. Then ![F[x]](https://s0.wp.com/latex.php?latex=F%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) , the set of all polynomials with coefficients from
, the set of all polynomials with coefficients from 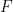 , forms a ring. For any
, forms a ring. For any ![f(x) \in F[x]](https://s0.wp.com/latex.php?latex=f%28x%29+%5Cin+F%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) with
with  , we define
, we define  where
where  means the
means the  -fold composition of
-fold composition of 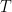 with itself. For any
with itself. For any  we define
we define  as
as 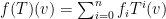 . Notice this satisfies the properties of a
. Notice this satisfies the properties of a ![F[x]](https://s0.wp.com/latex.php?latex=F%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) -module.
-module.

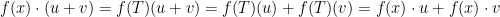
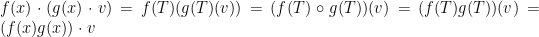
Thus this module, which we’ll denote  , has polynomials as its scalars.
, has polynomials as its scalars.
is an
-module, we say that
is a submodule of
if
is a subgroup of
and is closed under multiplication by elements of
. This can be summarized by saying that for every
and every
, the following two properties hold.
is an abelian group under addition, all subgroups are normal and we can form the quotient group
. This is naturally an abelian group, so in order to turn this into an
-module we have to define multiplication of elements in
and
, which we do in the most obvious way:
. To check that this is in fact an
-module, we simply verify that the three axioms of a module hold.
is a unitary module, then so too is
:
.
between two
-modules is a homomorphism if
is a group homomorphism with the additional property that for each
,
. As you would expect, the kernel of this homomorphism is a submodule of
, and the image is a submodule of
.
, we define
to be the smallest submodule of
containing
, which is naturally the intersection of all submodules containing
is a finite set, we may write
in place of
, and in the event that
is a singleton, we say that
is a cyclic submodule of
. We call the elements of
the generating set of the
submodule, and call the elements of
the generators of this submodule.
