A topological dynamical system is a pair 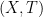 where
where  is a compact metric space and
is a compact metric space and  is a continuous map. This gives rise to an action of the semigroup
is a continuous map. This gives rise to an action of the semigroup  on
on  , where
, where 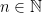 acts via the iterated map
acts via the iterated map 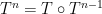 (and as usual
(and as usual  denotes the identity map). If
denotes the identity map). If 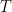 is invertible (i.e. a homeomorphism), then in fact it induces a
is invertible (i.e. a homeomorphism), then in fact it induces a 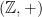 -action. More generally, one may consider an action
-action. More generally, one may consider an action 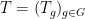 of any semigroup
of any semigroup  on
on  by continuous functions. This means that for each
by continuous functions. This means that for each  we have a continuous map
we have a continuous map 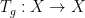 which satisfy the semigroup law
which satisfy the semigroup law  . In this case we say that
. In this case we say that 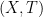 is a
is a  -system. Throughout this post I will denote by
-system. Throughout this post I will denote by  (or
(or  if the underlying space is clear) a compatible metric on
if the underlying space is clear) a compatible metric on  .
.
Two important classes of topological dynamical systems are the class of distal systems and the class of expansive systems.
While not entirely trivial, both properties are preserved by topological conjugacy (i.e., isomorphism in the category of  -systems), and in particular don’t depend on the choice of the (compatible) metric
-systems), and in particular don’t depend on the choice of the (compatible) metric  .
.
At a first glance at the definition it looks like the two conditions are quite similar. They both fall into the loose statement that “if two points are distinct, then they are far apart in the future” (at least if the acting semigroup is 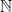 ). However, it turns out that the two properties are very much different, and in some sense actually incompatible.
). However, it turns out that the two properties are very much different, and in some sense actually incompatible.
In this post I will mention some examples and properties of distal and expansive systems which illustrate this difference between the two classes, and present a proof of the incompatibility result:
Theorem 2 An 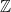 -system which is both distal and expansive must be finite. The same is true for
-system which is both distal and expansive must be finite. The same is true for 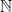 -systems.
-systems.
It is clear that any finite system (i.e., where  is a finite set) is both distal and expansive.
is a finite set) is both distal and expansive.
EDIT (25/03/2024): Sebastián Donoso informed me that an example of Meyerovitch and Salo (Example 2.6 in this paper) shows that the analogue of Theorem 2 does not hold for general  -systems.
-systems.
Continue reading →
be a measure preserving system and
a measurable set with
. For every
there exist
such that
.
is an arbitrary probability space and
any measurable map that preserves
. In the same paper Furstenberg also writes a dynamical reformulation for van der Waerden’s theorem (though it is not proved explicitly there that the two statements are equivalent).
be a minimal system and
open and non-empty. For every
there exists
such that
.
is a compact metric space and
is a homeomorphism such that every orbit
is dense. More generally one might consider compact Hausdorff spaces but it turns out that the apparently stronger statement is in fact equivalent to the one stated (ultimately because the statement uses only one set and its (countable) orbit, which therefore can all be realized in a metrizable factor).

