| CARVIEW |
Igor Pak's blog
On faith, religion, conjectures and Schubert calculus
Just in time for the holidays, Colleen Robichaux and I wrote this paper on positivity of Schubert coefficients. This paper is unlike any other paper I had written, both in the content and the way we obtained the results. To me, writing it was a religious experience. No, no, the paper is still mathematical, it’s just, uhm, different. Read this post till the end to find out how, or go straight to the paper (or perhaps both!)
Faith, religion and miracles — math got them all!
Mathematicians rarely if ever discuss the subject. When they do, they get either apologetic about it “there are no contradictions…”, or completely detached as if you can be deeply religious on Sunday morning and completely secular on Tuesday afternoon. See e.g. Robert Aumann’s extensive interview or this short clip by Freeman Dyson, two of the most admired people in their respective fields.
I have neither a religious education nor a specialized knowledge to speak on the subject, obviously. But in the age of Twitter (uhm, X.com, sorry) that minor issue never stopped anyone. So having said that, let me give a very vague and far-fetching primer to mathematicians in the language you could relate. This might prove helpful later on.
Faith is the foundation of it all. You really can’t do math without foundations. Outside of certain areas you don’t really need to understand it or even think about it all that that much. Just accept it and you’ll better off. For example, it is likely that the more you think about consistency of PA the less certain you get about what you are doing, so stay on the happy side.
This does not mean you need to be consistent with your owb tenants of faith. For example, it’s perfectly fine to have a paper in algebra using the Axiom of Choice (AC) while in another in descriptive set theory, where you go out of your way to avoid AC, and that’s the whole point of the paper. Still, it’s not like you were ever doubting AC — more like you have a multifaith personality.
Belief system is what it sounds like. If you are a working mathematician you probably already have a lot of opinions on a wide range of research questions, conjectures, etc. For example, maybe you accept some conjectures like Riemann Hypothesis, reject others like Navier-Stokes, remain very interested but undecided on problems like P vs. NP, and couldn’t care less about others like Yang-Mills. It’s all well and good, obviously.
There are many more shades of gray here. For example, you might believe in the abc conjecture, think that it hasn’t been proved yet, but willing to use it to prove other results whatever the status. Or perhaps, you believe that Goldbach’s conjecture is definitely true, that it’s a matter of time until it’s proved, but are completely unwilling to use it as an assumption (I used it as an assumption once, maddening some old school referees; luckily the odd version of GC holds and was sufficient). Or perhaps you are aware that the original proof of the Lyusternik-Schnirelmann theorem on three closed geodesics had major issues, as were many subsequent proofs of the theorem; still you are willing to trust Wikipedia that the theorem is true because you don’t care all that much anyway.
Ideally, you should question your beliefs whenever possible. If you are thinking about a conjecture, are you sure you believe in it? Maybe you should try to disprove it instead? It’s ok to change your mind, to try both directions, to believe or even to disbelieve all authorities on the matter. I have written extensively about the issue in this blog post, so let’s not rehash it.
One more thing about a belief system is that different beliefs usually have different levels of confidence. Some beliefs are core and people rarely change their mind. These don’t fall into faith category, in a sense that different people can have different core beliefs, sometimes in contradiction with each other. This is usually why a vast majority might strongly believe some conjecture is true, while a vocal minority might believe it’s false just as strongly.
For example, some people believe that mathematical order is absolutely fundamental, and tend to believe that various structures bring such an order. My core belief is sort of the opposite — because of whatever childhood trauma I experienced, I believe in universality theorems (sometimes phrased as Murphy’s law), that things can be wildly complicated to the extreme unless there is a good reason for them not to. Mnëv’s universality theorem is perhaps the most famous example, but there are many many others. This is why I disprove conjectures often enough and prove many NP– and #P-completeness results — these are different manifestations of the same phenomenon.
Religion is what you do with your belief system, as in practicing religion. If you have a lot of beliefs that doesn’t make you smart. That makes you opinionated. To be considered smart you need to act on your beliefs and actually prove something. To be considered wise you need the ability to learn to adjust your belief system to avoid contradictions with your other beliefs as new evidence emerges, and make choices that lead somewhere useful.
In mathematics, to practice an organized religion is to be professional, when you get paid for doing research. The process is fundamentally communal involving many people playing different roles (cf. this Thurston’s MO answer). Beside the obvious — researcher, editor, referee, publisher — there are many others. These include colleagues inviting you to give talks, departmental committees promoting you based on letter written by your letter writers. Some graduate students will be studying and giving talks on your work, others will be trying to simplify the arguments and extend them further. The list goes on.
In summary, it is absolutely ok to be an amateur and have your own religious practice. But within a community of like-minded scholars is where your research becomes truly valuable.
Miracles are the most delightful things that ever happen to you when learning or when doing mathematical research. It’s when you discover somethings, perhaps even prove that it works, but remain mystified as to why? What exactly is going on that made this miracle happen? Over time, you might learn one or several reasons, giving you a good explanation after the fact. But you have to remember your first impression when you just learned about the miracle.
It’s even harder to see and acknowledge miracles in celebrated textbook results. You have to train yourself to see the miracles for what they are, rather than for what they now appear to be when textbook packages them in neat nice boxes with a bow on top. One way to remind yourself of miracle powers is to read “Yes, Virginia“ column that I mentioned in this holiday post — it will melt you heart! Another way is to teach your favorites — when you see a joyful surprise in your students’ eyes, you know you just conveyed a miracle!
This may depend on your specific area, but in bijective combinatorics you have to believe in miracles! Otherwise you can never fully appreciate prior work, and can never let yourself loose enough to discover new miracles. To give just one example, the RSK correspondence is definitely on everyone’s the top ten list of miracles in the area. By now there are at least half a dozen ways to understand and explain it, but I still consider RSK to be a miracle.
Of course, one should not get overexcited about every miracle they see and learn to look deeper. For example, a combinatorial interpretation of Littlewood–Richardson coefficients is definitely a miracle, no doubt about it. But after some meditation you may realize that it’s really the same miracle as RSK (see §11.4 in my OPAC survey).
Backstory of the bunkbed conjecture paper
After I wrote this blog post about our disproof of the Bunkbed Conjecture (BBC), the paper became viral for 15 minutes. Soon after, I received several emails and phone calls from journalists (see links in the P.P.S. of that post). They followed the links to my earlier blog post about disproofs of conjectures and asked me questions like “What is the next conjecture do you plan to disprove?” and “Do you think disproving conjectures is more important than proving them?” Ugh… 😒
While that earlier post was written in a contrarian style, that was largely for entertainment purposes, and not how I actually think about math. Rather, I have an extensive somewhat idiosyncratic belief system that sometimes leads me think that certain conjectures are false. But breaking with conventional wisdom is a long and occasionally painful process. Worse, being a contrarian gives you a bad rap as you are often get confused with being nihilistic.
So let me describe how I came to believe that BBC is false. I was asked this multiple times, always declining out of fear of being misunderstood and misquoted. but it’s a story worth telling.
This all started with my long FOCS paper (joint with Christian Ikenmeyer), where we systematically studied polynomial inequalities and developed a rather advanced technology to resolve questions like “which of these can be proved combinatorially by a direct injection?” To give a basic example, if the defect (difference between two sides) is a polynomial that is an exact square, then the polynomial is obviously nonnegative but it often can be shown that the defect has no combinatorial interpretation, i.e. not in #P. See more in this blog post on this.
Now, I first learned about the Bunkbed Conjecture soon after coming to UCLA about 15 years ago. Tom Liggett who was incredibly kind to me, mentioned it several times over the years, always remarking that I am “the right person” to prove it. Unfortunately, Tom died just four years ago, and I keep wondering what he would have made of the story…
Anyway, when writing my OPAC survey two years ago, I was thinking about the problem again in connection to combinatorial interpretations, since BBC becomes a polynomial inequality when all edge probabilities are independent variables. Like everyone else, I assumed that BBC is true. But I figured that the counting version is not in #P since otherwise a combinatorial proof would have been found already (since many strong people have tried). So I made this into Conjecture 5.5 in the OPAC paper, and suggested it to my PhD student Nikita Gladkov.
I believed at that time that there must be a relatively small graph on which the BBC defect will be a square of some polynomial, or at least some positive polynomial (on a [0,1]n hypercube of n variables) with negative coefficients. That was our experience in the FOCS paper. Unfortunately, this guess was wrong. In our numerous experiments, the polynomials in the defect seemed to have positive coefficients without an obvious pattern. It was clear that having a direct injective proof would have been a miracle, the kind of miracle that one shouldn’t expect in the generality of all graphs.
This led to a belief contradiction — either a stronger version of BBC holds for a noncombinatorial reason, or BBC is false. In the language above, I had a core belief in the power of combinatorial injections when there are no clear obstructions. On the other hand, I had only a vague intuition that BBC should hold because it’s the most natural thing and because if true it would bring a bit of order to the universe. So I changed my mind about BBC and we started looking for a counterexample.
Over the next two years I asked about BBC to everyone I met, suggesting that it might be false in hope someone, anyone, gives a hint on how to proceed and what to rule out. Among those who knew and had an opinion about the problem, everyone was sure it’s true. Except for Jeff Kahn who lowered his voice and very quietly told me that he also thinks it’s false, but made me a promise not to tell anyone (I hope it’s ok now?) I think he was hinting I shouldn’t say these things out loud to avoid getting the crank reputation. I didn’t listen, obviously. Not being in the area helped — nobody took me seriously anyway.
In the meantime, Nikita and his friend Alexander Zimin made quite a bit of effort to understand multiple correlation inequalities (FKG style) for percolation on general graphs. This eventually led to the disproof as explained in the BBC blog post mentioned above.
Schubert positivity
In Algebraic Combinatorics, Schubert coefficients are nonnegative integers which generalize the Littlewood-Richardson (LR) coefficients mentioned above. Since the latter have extremely well studied combinatorial interpretations, the early hope was that Schubert coefficients would also have one. After decades of effort and advances in a handful of special cases, this became a major open problem in the area, the subject of numerous talks and papers.
I never believed this hope, not for a second. In the OPAC survey, I stated this as a conjecture: “Schubert coefficients are not in #P” (see Conj. 10.1). Again, this not because I was a contrarian — I had my reasons, three in fact.
First, that’s because I studied the miracle of RSK and the related miracle of LR-coefficients for over thirty years (yes, I am that old!) As a bijection, RSK is extremely rigid. So if any of the (essentially equivalent) combinatorial interpretations of LR-coefficients could generalize directly, it would have been done already. However, the progress has been exceedingly difficult (see e.g. Knutson’s 2022 ICM paper).
Second, I also have a strong belief that miracles are rare and don’t happen to the same combinatorial objects twice for different reasons. This is a variation on “lightening doesn’t strike twice” idea. It is in principle possible that LR-coefficients have a completely new combinatorial interpretation radically different from the 20+ combinatorial interpretations (see OPAC survey, §11.4), all of them related by relatively easy bijections. But I had my doubts.
Third, I knew quite a bit about efforts to find a combinatorial interpretation for Kronecker coefficients which also generalize LR-coefficients in a different direction. Joint with Greta Panova, I have written extensively on the subject. I was (still am) completely confident that Kronecker coefficients are not in #P for many reasons too long to list (this is Conjecture 9.1 in my OPAC survey). So I simply assumed that Schubert coefficients are also not in #P, by analogy.
Having concluded that one should work in the negative direction, Colleen and I made a major effort towards proving that Schubert coefficients are not in #P, aiming to emulate the strategy in my paper with Chan, and in earlier work with Ikenmeyer and Panova. The basic idea is to show that the positivity problem is not in the polynomial hierarchy PH, which would imply that the counting problem is not in #P. We failed but in a surprisingly powerful way which led me to rethink my whole belief system when it comes to Schubert calculus.
By the Schubert positivity problem we mean the decision problem that Schubert coefficients are positive. This problem is a stepping stone towards finding a combinatorial interpretation, and is also of independent interest. In our previous paper with Colleen, we proved that the positivity problem is in the complexity class AM assuming the Generalized Riemann Hypothesis (GRH). This is a class that is sandwiched between first and second level of the polynomial hierarchy, so in particular in contains NP and BPP, and is contained in Π2. In particular, my dream of proving that the positivity problem is not in PH was doomed from the start (assuming PH does not collapse).
Now that that Schubert positivity is in PH this explains the earlier failures, but leaves many questions. First, should we believe that Schubert coefficients are in #P? That would imply that Schubert positivity is in NP, a result we don’t have. Second, where did we go wrong? Which of my beliefs were mistaken, and what does that say about the rest of my belief system?
Let me start with the second which easier to answer. I continue to stand by our first belief (the miracle of RSK and LR) — this is going nowhere. I am no longer confident in the second belief. It is possible that #P is so much larger than traditional combinatorial interpretations that there is more to the story. And lightnings can strike twice if the buildings are especially tall…
More importantly, I now completely reject the third belief of analogy between Kronecker and Schubert coefficients. While the former is fundamentally representation-theoretic (RT), as our proof shows the latter is fundamentally algebro-geometric (AG). They have nothing in common except for the LR-coefficients. At the end, while we proved that Schubert positivity is in AM (assuming GRH) using the Hilbert’s Nullstellensatz, a key problem in AG.
Faced with a clash of core beliefs, Colleen and I needed to completely rethink the strategy and try to explain what do our results really mean? Turned out, my issues were deeper than I thought. At the time I completely lacked faith in derandomization, which is getting close to be a foundation belief in computational complexity, on par with P ≠ NP. I was even derisive about it in the P.S. to my BBC blog post.
On a personal level, saying that P = BPP is weird, or at least unintuitive. It contradicts everything I know about Monte Carlo methods used across the sciences. It undermines the whole Markov chain Monte Carlo technology I worked on in my PhD thesis and as a postdoc. I even remember a very public shouting match on the subject between the late Steven Rudich and my PhD advisor Persi Diaconis — it wasn’t pretty.
After talking to Avi Wigderson while at IAS, I decided to distance myself and think rationally rather than emotionally. Could P = BPP be really true? Unless you know much about derandomization, even P = ZPP seems unmotivated. But these conjectures have a very good reason in their favor.
Namely, the Impagliazzo–Wigderson’s theorem says that under a reasonable extension of the exponential time hypothesis (EHT), itself an advance extension of P ≠ NP, we have P = BPP. Roughly speaking, if hard NP problems are truly hard (require exponential size circuits), one can simulate binary strings by embedding meshed up solutions into the strings which then look random in a sense of poly-time algorithms can’t tell them apart. This is extremely vague and somewhat misleading — read up more on this in Vadhan’s monograph (Chapter 7).
There is also a CS Theory community based argument. In this 2019 poll conducted by Gasarch, there is near unanimous 98% belief that P = BPP by the “experts” (others people were close to even split). Given that P ≠ NP has 99% belief by the same experts, this crosses from speculation to the standard assumption territory. So it became clear that I should completely switch my core belief from P ≠ BPP to P = BPP.
And why not? I have blindly believed the Riemann Hypothesis (RH) for decades without any in-depth knowledge of analytic number theory beyond a standard course I took in college. I am generally aware of applications of RH across number theory and beyond, see quotes and links here, for example. From what I can tell, RH withstood all attempts to disprove it numerically (going back to Turing), and minor dissents (discussed here) do not look promising.
This all reminded me of a strange dialogue I had with Doron Zeilberger (DZ) over lunch back in October, when we went to celebrate the BBC disproof:
DZ: What conjectures do you believe? Do you believe that RH is true?
IP: I am not sure. Probably, but I don’t have enough intuition either way.
DZ: You are an idiot! It’s 100% true! Do you believe that P ≠ NP?
IP: Yes, I do.
DZ: Ok, you are not a complete idiot.
Anyway, back to the story. I figured that if you believe in RH you may as well believe in GRH. And if you believe in P ≠ NP you may as well believe in ETH. And if you believe in ETH you may as well believe in the Impagliazzo–Wigderson’s Assumption (IWA) which implies that P = BPP. And if you believe in IWA you may as well believe in the Miltersen–Vinodchandran Assumption (MVA) which is an interactive proof version of IWA introduced in this paper, and which implies that NP = AM. Once you break this it into steps, the logic of this implication becomes clear and the conclusion extremely believable.
Having thought through these implications, Colleen and I wrote this note which prompted this blog post. We aim at people in algebraic combinatorics and obtain the following:
Main Theorem [Robichaux–P.] Schubert positivity is in NP (i.e., has a positive rule) assuming GRH and MVA.
The theorem is the closest we got to proving that Schubert coefficients are in #P. The note is written in a somewhat unusual style, explaining the results and refuting potential critiques. Quotes by Poincaré and Voltaire are included in support of the case. Check it out!
In summary, the theorem above completely resolves the Schubert positivity problem albeit conditionally and from computational complexity point of view. It assumes two very hard conjectures, each stronger than a million dollar problem. But so what? It’s not even the first theorem which assumes two million dollars worth of conjectures (it’s a long article — search for “two million dollars”). And with inflation, one million in 2000 is about two millions now, so it’s probably ok to assume two such conjectures in one theorem anyway… 😉
Happy Holidays! Happy New Year! Best wishes everyone!
Concise functions and spanning trees
Is there anything new in Enumerative Combinatorics? Most experts would tell you about some interesting new theorems, beautiful bijections, advanced techniques, connections to other areas, etc. Most outsiders would simply scoff, as in “what can possibly be new about a simple act of counting?” In fact, if you ask traditional combinatorialists they would be happy to tell you they they like their area to be trend-resistant. They wouldn’t use these words, obviously, but rather say something about timeless, or beautiful art, or “balls in boxes”. The following quote is a classic of this genre:
Combinatorialists use recurrence, generating functions, and such transformations as the Vandermonde convolution; others, to my horror, use contour integrals, differential equations, and other resources of mathematical analysis. (J. Riordan, Combinatorial identities, 1968)
If you’ve been reading this blog for a while, then you already know how I feel about such backward-looking views. When these win, the area becomes stale, isolated, and eventually ignored by both junior researchers and the “establishment” (leading math journals, granting agencies, etc.) Personally, I don’t I don’t see this happening in part due to the influence of Theoretical Computer Science (TCS) that I discussed back in 2012 in this blog post.
In fact, the influence of TCS is so great on all aspects of Combinatorics (and Mathematics in general), let me just list three ideas with the most impact on Enumerative Combinatorics:
- Thinking of a “closed formula” for a combinatorial counting function as algorithm for computing the function, leading to Analysis of Algorithms type analysis (see Wilf’s pioneer article and my ICM paper).
- The theory of #P-completeness (and related notions such as #P-hard, #EXP-complete, class GapP, etc.) explaining why various functions do not have closed formulas. This is now a core part of Computational Complexity (see e.g. Chapter 13 in this fun textbook).
- The idea that a “combinatorial interpretation” is simply a function in #P. This is my main direction these days, see this blog post, this length survey and this OPAC talk and this StanleyFest talk.
All three brought remarkable changes in the way the community understands counting problems. In my own case, this led to many interesting question resulting in dozens on papers. Last year, in the middle of a technical complexity theoretic argument, I learned of a yet another very general direction which seem to have been overlooked. I will discuss it briefly in this blog post.
Complete functions
Let A be a set of combinatorial objects with a natural parametrization: A = ∪ An. For example, these can be graphs on n vertices, posets on n elements, regions in the square grid with n squares, etc. Let f: A → N be a function counting objects associated with A. Such functions can be, for example, the number of 3-colorings or the number of perfect matchings of a graph, the number of order ideals or the number of linear extensions of a poset, the number of domino tilings of a region, etc.
We say that f is complete if f(A)=N. Similarly, f is almost complete if f(A) contains all sufficiently large integers. For example, the number of perfect matchings of a simple graph is complete as can be seen from the following nice construction:

Moreover, the number of domino tilings of a region in Z2 is complete since for every integer k, there is a staircase-type region like you see below with exactly k domino tilings (this was observed in 2014 by Philippe Nadeau).

In fact, most natural counting functions are either complete or almost complete. For example, the number of spanning trees of a simple graph is almost complete since the number of spanning trees in an n-cycle is exactly n, for all n>2. Similarly, the number of standard Young tableaux |SYT(λ)| of a partition λ is almost complete since |SYT(m,1)|=m. Many other natural examples are in our paper with Swee Hong Chan (SHC) which started this investigation.
Concise functions
Let f be an almost complete function. We say that f is concise if for all large enough k, there exist an element a ∈ An such that f(a) = k and n < C (log k)c, for some C, c>0. Just like explicit constructions in the context of Graph Theory (made famous by expanders), this notion makes perfect sense irrespectively from our applications in computational complexity (see our paper with SHC linked above).
Note that none of the simple constructions mentioned above imply that the corresponding functions are concise. This is because the size of combinatorial objects is linear in each case, not poly-logarithmic as we need it to be. For the number of perfect matchings, an elegant construction by Brualdi and Newman (1965) shows that one can take n = O(log k). This is the oldest result that we know, that some natural combinatorial counting function is concise.
For the number of domino tilings, SHC and I proved an optimal bound: there is a region with O(log k) squares with exactly k domino tilings. The proof is entirely elementary, accessible to a High School student. The idea is to give explicit transformations k → 2k and k → 2k-1 using gadgets of the following kind:

As always, there are minor technical details in this construction, but the important takeaway is that we obtain an optimal bound, but the regions we construct are not simply-connected. For simply-connected regions the best bound we have is O(log k log log k) for the snake (ribbon) regions, via connection to continued fractions that was recently popularized by Schiffler. Whether one can obtain O(log k) bound in this case is an interesting open problem, see §6.4 in our paper with SHC.
Many concise functions
For the number of spanning trees, whether this function is concise remained an open problem for over 50 years. Even a sublinear bound was open. The problem was recently resolved by Stong in this beautiful paper, where he gave O((log k)3/2/(log log k)) upper bound. Sedláček (1967) conjectured that o(log k) bound for general graphs, a conjecture which remains wide open.
For some functions, it is easy to see that they are not concise. For example, for a partition λ of n, the number of standard Young tableaux |SYT(λ)| is a divisor of n! Thus, for k prime, one cannot take n<k in this case.
Curiously, there exist functions, for which being almost complete and concise are equivalent notions. For example, let T ∈ R2 be a set of n points in general positions in the plane. Denote by g(T) the number of triangulations of T. Is g almost complete? We don’t know but my guess is yes, see Conjecture 6.4 in our paper with SHC. However, we do know exponential lower and upper bounds Cn < g(T) <Dn. Thus, if g is almost complete it is automatically concise with an optimal O(log k) upper bound.
Our final example is much too amusing to be skipped. Let e(P) denote the number of linear extensions of a poset on n elements. This function generalized the number of standard Young tableaux, and appears in a number of applications (see our recent survey with SHC). Tenner proved a O(√k) bound, the first sublinear bound. The conciseness was shown recently by Kravitz and Sah, where they established O(log k log log k) upper bound. The authors conjectured O(log k) bound, but potentially even O((log k)/(log log k)) might hold.
Consider now a restriction of the function e to posets of height two. In our paper with SHC, we have Conjecture 5.17 which claims that such e is still almost complete. In other words, for all large enough k, one can find a poset of height two with exactly k linear extensions. Since the number of linear extensions of such posets is at least (n/2)!2 this would give an optimal bound for general posets as well, so a very sharp extension of the Kravitz–Sah bound. We should mention an observation of Soukup (p. 80), that 13,168,189,439,999 is not the number of linear extensions of a height two poset. This suggests that our conjecture is either false, or likely to be very hard.
Latest news: back to spanning trees
In our most recent paper with Swee Hong Chan and Alex Kontorovich, we resolve one Sedláček’s question and advance another. We study the number τ(G) of spanning trees in a simple planar graph G on n vertices. This function τ is concise by Stong’s theorem (his construction is planar), and it is easy to show by planarity that τ(G) < 6n. Thus, a logarithmic upper bound O(log k) is the best one can hope for. Clearly, proving such result would be a major advancement over Stong’s poly-logarithmic bound.
While we don’t prove O(log k) bound, we do get very close — we prove that this bound holds for the set of integers k of density 1. The proof is both unusual (to me as a combinatorialist), and involves a mixture of graph theory, number theory, ergodic theory, and some pure luck. Notably, the paper used the remarkable Bourgain–Kontorovich technology developed towards the celebrated Zaremba’s Conjecture. You can read it all in the paper or this longish post by Alex.
P.S. Being stubborn and all, I remain opposed to the “unity of mathematics” philosophy (see this blog post which I wrote about the ICM before later events made it obsolete). But I do understand what people mean when they say these words — something like what happened in our paper with Alex and Swee Hong with its interdisciplinary tools and ideas. And yet, to me the paper is squarely in Combinatorics — we just use some funky non-combinatorial tools to get the result.
Princeton President to Princeton Jews: For the sake of free speech please shut up!
The readers of this blog know know that I stay away from non-math related discussions. It’s not that I don’t have any political opinions, I just don’t think they are especially valuable or original. I do however get triggered by a clear anti-Semitism, discrimination of Jews by the universities, and by personal disrespect. The story below is a strange mixture of these.
As I was visiting the IAS in Princeton, I had the dubious fortune to attend a speech by Christopher Eisgruber last week. Eisgruber has been Princeton’s President since 2013 and a long time Princetonian. To say I was disappointed is to say nothing — I was appalled by the condescension and the lack of empathy. But I think President Eisgruber left feeling that it was a successful event. Let me set the scene first before I explain what happened.
Last Saturday was Yom Kippur, the holiest day in the Jewish calendar, the day of atonement and repentance. This is also a day of remembering the dead, and there were a lot of deaths to remember this year. This is also a day to recognize rising antisemitism and pray for peace.
President Eisgruber was invited to speak at the Jewish Center, Princeton’s leading Conservative congregation. I think he was invited not as an expert on Constitutional Law (which he is), but as a President of a major research university with a sizable Jewish community that has been suffering for the past year and is in desperate need of healing.
It seems, President Eisgruber had not noticed. The speech he chose to give was on freedom of speech and how great (well, excellent!) Princeton is doing in that regard (oh, joy!) And how happy and satisfied was the Princeton Jewish community in the past year (wait, what? really?)
President Eisgruber explained at great length the importance of free speech, including the offensive speech. That it’s vital for productive debate. That as a private university Princeton could do more, of course, but he is absolutely uninterested in policing speech beyond constitutional requirements.
Now, I spent over 30 years in academia in the US, so I heard it all before. Probably everyone in academia has. It’s fine in the abstract. The reality is different. By now, everyone on a major university campus is well familiar with universities’ proclivities towards protecting one kind of speech and not protecting the other. Eisgruber’s speech was epitome of this hypocrisy, highlighted by the setting and aggravated by insensitivity of his answers.
During the Q&A, President Eisgruber clarified that all those anti-Israel slogans like “from the river to the sea…” and “globalize the intifada” that were heard on campus are nothing to worry about. Because you see, they have a committee which looked at those slogans and concluded they are not anti-Semitic, at least not always (depending on the context, perhaps?) Because even The New York Times (apparently, a reputable authority on the subject) concluded that these slogans mean different things to different people, so it’s all good. In fact, he continued,
I sincerely believe that even the majority of those who said these things are not anti-Semitic.
Whether he believes it’s ok to have an anti-Semitic minority on Princeton campus was never clarified.
At this point President Eisgruber hedged and said that “we must remember” that it’s not about whether the Jewish community is offended, but rather whether the speech is constitutionally permissible. Without ever disclosing his personal views, he double-hedged and mentioned one Middle Eastern scholar at Princeton, who suggested that these slogans are simply in bad taste. And like all things Princetonian, that scholar must be the world’s leading authority (I am paraphrasing).
President Eisgruber then triple-hedged and mentioned that he “promised to the general council” to say that those who are still aggrieved should not ask him (“I don’t decide these things”), but rather can again petition that all-powerful committee presiding over permissible speech. He slyly smirked at the audience and suggested that if we lose that’s also ok, because being offended is just part of life…
When a brave Princeton faculty asked for his views on speech against other marginalized communities, he was unable to get out of the hole he just dug for himself. So he chose to lie. He said he would be ok to have such an offensive speech, that it really doesn’t matter against what community is the speech. Not a soul in the audience believed him, obviously, even the 13 year olds knew better.
Asked to give examples, he stiffened for a second, but then started stalling. He recalled a booth on a sidewalk which spewed ani-gay propaganda at students. He admitted that of course that booth was on public property, so even if he wanted to shut it down he couldn’t. But even if he could, maybe he wouldn’t, that even though he hated that speech, it was allowed under the Constitution, although it did make bad news at the time, but that’s ok. Ugh… At that point, the answer lasted long enough for the audience to forget what was the question, which was the intent I presume.
Most appallingly, President Eisgruber explained to us that apparently the Princeton Jewish community is “thriving”. Are you sure that Princeton students are any different in their views from the UC students, Mr. President? Although this is his first time ever giving a talk in a synagogue (he thought he was bragging, I think), he “had seen student surveys” which proved that
Last year, the Jewish students at Princeton were more satisfied than in previous years.
He didn’t give any numbers, so it’s hard to know what level of satisfaction is he even talking about. How bad exactly were these numbers to begin with, that they hadn’t significantly dropped? Please make them public, so we can take a look! For example, in 2022 UCLA did make their surveys public and we can easily read the bottom of this table:

What President Eisgruber is saying is so much contrary to common sense, you have to be blind, deaf and have no access to social media to believe that. A simple Google search would suggest that Princeton Has Become a Hostile Place for Jews and produce this report card. There is even an official Title VI investigation by the US Department of Education into into Princeton over alleged antisemitism on campus. Great job, Mr. President!
I would be amiss to say that President Eisgruber showed no empathy at all. He did, when he lamented:
I feel so bad for presidents of other universities who had to testify for three hours under bright lights!
I don’t think either of these presidents were in the audience, but I am sure they would have appreciated the sentiment. (Full disclosure: UCLA former Chancellor Gene Block also testified to the House Committee.)
Now, university presidents are basically politicians. Good politicians know how to read the audience and can fake empathy. Bad politicians recycle old speeches written for donors and dwell on tedious legal details. Clearly, President Eisgruber is either a really terrible politician, or has been at the job for so long that he simply stopped caring.
I have several theories of what happened. Maybe he thought that his story of a Holocaust survivor grandfather would give him cover to say anything. Or maybe he thought that this was a private event closed to outsiders, and these Princeton Jewish folks are just too invested in the community to voice a protest. Or maybe he just loves Constitutional Law and has nothing else to say. Perhaps, all of the above.
But my favorite theory is that he thought he was helping. Clearly, after you tell people who are suffering “don’t feel bad” they will feel an instant relief, right? Because, you see, whatever we are feeling is not Princeton University’s fault, it’s all fault of the ever so binding US Constitution…
I hate to speculate if President Eisgruber gives the same kind of speeches to other marginalized communities. But if that’s the case, maybe it’s time to follow all those “other university presidents” and resign. Let us grieve and suffer in peace without you lecturing us on how we should feel and admonishing us for wanting equal treatment or just to feel safe on campus.
You clearly care a great deal about the law, Mr. President, so maybe you can get back to doing it full time? Please leave the presidency to someone who has at least an ounce of empathy.
The bunkbed conjecture is false
What follows is an unusual story of perseverance. We start with a conjecture and after some plot twists end up discussing the meaning of truth. While the title is a spoiler, you might not be able to guess how we got there…
The conjecture
The bunkbed conjecture (BBC) is a basic claim about random subgraphs. Start with a finite graph G=(V,E) and consider a product graph G x K2 obtained by connecting the corresponding vertices on levels V(1) and V(2). Sort of like a bunkbed. Now consider random subgraphs of a this product graph.
Bunkbed Conjecture: The probability that vertices u(1) and v(1) are connected is greater or equal than the probability that vertices u(1) and v(2) are connected.
In other words, the probability of connecting two vertices on the same level cannot be smaller than when connect vertices on different levels. This is completely obvious, of course! And yet the conjecture this problem defeated several generations of probabilists and remained open until now. For a good reason, of course. It was false!
The origins of the conjecture are murky, but according to van den Berg and Kahn it was conjectured by Kasteleyn in the early 1980s. There are many versions of this conjecture; notably one can condition on the subset of vertical edges and ask the same question. Many partial results are known, as well as results for other probabilistic models. The conjecture is false nonetheless!
The direction
Why look for a counterexample if the conjecture is so obviously true? Well, because you always should. For any conjecture. Especially if everyone else is so sure, as in completely absolutely sure without a doubt, that the conjecture is true. What if they are all wrong? I discuss this at length in this blog post, so there is no need to rehash this point.
The counterexample
We disprove the conjecture in a joint paper with Nikita Gladkov (UCLA) and Alexandr Zimin (MIT), both graduate students. Roughly speaking we take the following 3-hypergraph from a recent paper by Hollom.

We then replace each yellow triangle with the following gadget using n=1204, placing a in the shaded vertex, while v1 and vn are placed in the other vertices of the triangle (so the red path goes into the red path). For a stronger version of the conjecture that’s all there is. For a weaker version, some additional tweaks needed to be made (they are not so important). And we are done!

The resulting graph is has 7523 vertices and 15654 edges. The difference between probabilities for paths between u1 and u10 at the same and different levels as in the conjecture is astronomically small, on the order of -10-6500. But it’s negative, which is all we need. Very very roughly speaking, the red path is the only path which avoids shaded vertices and creates a certain bias which give this probability gap. Formalizing this is a bit technical.
The experiments
Of course, the obvious way to verify our counterexample computationally would fail miserably — the graph is much too large. Instead, we give a relatively elementary completely combinatorial disproof of the BBC that is accessible to a wide audience. I would rather not rehash technical details and ideas in the proof — it’s all in our paper, which is only 12 pages! See also the GitHub code and some explanation.
I do want to mention that giving formal disproof was not our first choice. It’s what we ended up doing after many failures. There is always a bit of a stigma people have about publicly discussing their failures. I know very few examples, only this one famous enough to be mentioned. So let me mention briefly how we failed.
Since I was sure the bunkbed conjecture is false (for reasons somewhat different from my contrarian philosophy), we started with a myriad of computer experiments trying all small graphs. When those failed, we tried to use AI and other computer assisted tools. We burned many hours on a giant UCLA Hoffman2 Cluster getting closer for a while. In hindsight, we didn’t look in the right place, obviously. After several months of computer experiments and no clear counterexample, it felt we are wasting time. We then thought a bit more about philosophy of what we are doing and stopped.
Before I tell you why we stopped, let me make a general recommendation. Please do try computer experiments for whatever you are working on. Make an effort to think it through and design a good experiment. Work hard to test as much as your computer technology allows. If you need some computing power, ask around. Your university might just have the resources. Occasionally, you can even ask a private company to donate theirs.
If you succeed, write a paper and publish it. Make your code and work notes publicly available. If you fail, do exactly the same. If the journals refuse to publish your paper, just keep it on the arXiv. Other people in your area would want to know. And as far as the NSF is concerned, all of this is “work product”. You can’t change the nature of the problem and the results you are getting, but you deserve the credit regardless.
Let me repeat: Do not fear telling other you have not succeeded in your computer testing. Fear others making the same mistakes or repeating the same work that you did.
The curse
One reason we stopped is because in our initial rush to testing we failed to contemplate the implications of Monte Carlo testing of even moderately large graphs. Here is a quote from the paper:
Suppose we did find a potential counterexample graph with only m=100 edges and the probability gap was large enough to be statistically detectable. Since analyzing all of 2m ≈ 1030 subgraphs is not feasible, our Monte Carlo simulations could only confirm the desired inequality with high probability. While this probability could be amplified by repeated testing, one could never formally disprove the bunkbed conjecture this way, of course.
This raises somewhat uncomfortable questions whether the mathematical community is ready to live with an uncertainty over validity of formal claims that are only known with high probability. It is also unclear whether in this imaginary world the granting agencies would be willing to support costly computational projects to further increase such probabilities (cf. [Garrabrant+’16], [Zeilberger’93]). Fortunately, our failed computational effort avoided this dystopian reality, and we were able to disprove the bunkbed conjecture by a formal argument.
Societal implications aside, it is an interesting question whether a reputable math journal should accept a counterexample that is tested with 99.99% confidence, and the results can be replicated and rechecked by others. Five sigma may be a gold standard in nuclear physics, but math journals tend to prefer 100% correctness (even though some papers they publish are 100% incorrect).
What I do know, is that most journals would refuse to even consider a “five sigma counterexample”. While details of the situations differ quite a bit, I knew what happened to the (rather interesting) Sills–Zeilberger paper, which was eventually published, but not after several desk rejections. But PhD students need jobs in reality, not in theory. That is really why we stopped. Why persevere and create controversy when you can just try doing something else?
P.S. There is yet another layer to all of this. Back in 1999, I asked Avi Wigderson if P=BPP? He said “Yes“. Last week I asked him again. This is 25 years later, almost to the day. He said “Yes, I am absolutely sure of that.” It’s one of his favorite conjectures, of course. If he is right, every probabilistic counterexample can be turned into deterministic. In other words, there would be a fully rigorous way to estimate both probabilities and prove on a computer that the conjecture is false. But you must have guessed what I was thinking when I heard what he said — now he used “absolutely sure“…
P.P.S. There is a very nice YouTube video about our paper made by Trefor Bazett. Another (even better) YouTube video by Johann Beurich (in German). See also this article in Quanta Magazine, this in IFLScience, that in Pour la Science (in French) and that in Security Lab (in Russian) about our work and this blog post.
UPDATE (June 13, 2025). This took awhile, but the paper was just published at PNAS.
We deserve better journals
By and large, math journals treat the authors like a pesky annoyance, sort of the way a local electric company treats its customers. As in — yes, serving you is our business, but if you don’t like our customer service where else are you going to go? Not all editors operate that way, absolutely not all referees, but so many it’s an accepted norm. We all know that and all play some role in the system. And we all can do better, because we deserve better.
In fact, many well meaning mathematicians do become journal editors, start new journals, and even join the AMS and other professional societies’ governing bodies which oversee the journals. This helps sometimes, but they quickly burn out or get disillusioned. At the end, this only makes second order improvements while the giant sclerotic system continues its descent from bad to worse.
Like everyone else, I took this as a given. I even made some excuses: evil publishers, the overwhelming growth of submissions, everyone stressed and overworked, papers becoming more technical and harder to referee, etc., etc. For decades I watched many math journals turn from friendly if not particularly warm communal endeavors, to zones of hostility.
Only most recently, it occurred to me that it doesn’t have to be this way. We should have better journals, and we deserve a better treatment (I was really off the mark in my first line of this post). Demanding better journals is neither a fantasy nor a manifesto. In fact, physicists have already figured it all out. This post is largely about how they do it, with some lessons and suggestions.
What we have
If you don’t know what I am talking about, walk to any mathematician you see at a conference. If you have a choice, choose the one who looks bored, staring intensely at their shoes. Ask them for their most frustrating journal publishing story. You may as well sit down — the answer might take awhile. Even if they don’t know you (or maybe especially if they don’t know you), they will just unload a litany of the most horrifying stories that would make you question the sanity of people staying in this profession.
Then ask them why do they persevere and keep submitting and resubmitting their papers given that the arXiv is a perfectly fine way to disseminate their work. You won’t hear a coherent answer, but rather the usual fruit salad of practical matters: something about jobs, CVs, graduate students, grants, Deans, promotions, etc. Nobody will ever mention that their goal is to increase their readership, verify the arguments, improve their presentation style, etc., ostensibly the purpose of mathematical journals.
While my personal experience is a relatively happy one, I do have some scars to show and some stories to tell (see this, that and a bit in that blog posts on publishing struggles). There is no need to rehash them. I also know numerous stories of many people because I have asked them these questions. In fact, every time I publish something like this blog post (about the journals’ hall of shame), I get a host of new horror stories by email, with an understanding that I am not allowed to share them.
The adversarial relationship and countless bad experiences make it is easy to lose sight of the big picture. In many ways we are privileged in mathematics to have relatively few bad and for-profit actors. Money and grant funding matters less. We don’t have extreme urgency to publish. We have some relatively objective ways to evaluate papers (by checking the proofs). One really can work on the Moon, as long as one has a laptop and unlimited internet (and breathable air, I suppose).
We have it good, or at least we did when we started sliding into abyss. Because the alarms are not ringing, the innovation in response has stuttered. We are all just chugging along. Indeed, other than a few new online journals, relatively little has changed in the past two decades.
This is in sharp contrast with physics, which had very few of the advantages that math has (depending on the area). Besieged on all sides, physics community was forced to adapt faster and arguably better in response to changes in the publishing landscape. In fact, the innovations they made are so natural to them, their eyes open wide in disbelief when they hear how we continue to publish math papers.
The following is a story of the Physical Review E (PRE), one of the journals of the American Physical Society (APS). I will start with what I learned about the PRE and APS inner working, their culture, successes and challenges, some of which ring very familiar. Only afterwards I will get back to math publishing, the AMS and how we squandered our advantages.
What’s special about PRE?
I chose to write about the PRE because I published my own paper there and enjoyed the experience. To learn more about the journal, I spoke to a number of people affiliated with PRE in different capacities, from the management to members of the Editorial Board, to frequent authors and reviewers. These interviews were rather extensive and the differences with the math publishing culture are much too vast to summarize in a single blog post. I will only highlight things I personally found remarkable, and a few smaller things that can be easily emulated by math journals.
PRE’s place in the physics journal universe
PRE is one of five similarly named “area journals”: PRA, PRB, etc. More generally, it is one of 18 journals of the APS. Other journals include Physical Review Letters (PRL is APS’s flagship journal which published only very short papers), Physical Review X (PRX is another APS’s leading journal, online only, gold open access, publishes longer articles, extremely selective), Reviews of Modern Physics (APS’s highest cited journal which publishes only survey articles), and a number of more specialized journals.
The APS is roughly similar to the the AMS in its prominence and reach in the US. APS’s main publishing competition include the Institute of Physics (IOP, a UK physics society with 85 titles, roughly similar to the LMS), Nature Portfolio (a division of Springer Nature with 156 titles only a few of them in physics), and to a lesser extent Science by AAAS, various Elsevier, SIAM journals, and some MDPI titles.
Journal structure
The PRE editorial structure is rather complicated. Most of the editorial work is done by an assortment of Associate Editors, some of whom are employed full time by the APS (all of them physics PhD’s), and some are faculty in physics or adjacent fields from around the world, typically full time employed at research universities. Such Associate Editors receive a 2 year renewable contract and sometimes work with the APS for many years. Both professional and part time editors do a lot of work handling papers, rejecting some papers outright, inviting referees, etc.
The leadership of PRE is currently in flux, but until recently included Managing Editor, a full time APS employee responsible for running the journal (such as overseeing the work of associate editors), and a university based Lead Editor overseeing the research direction. The APS is currently reviewing applications for a newly created position of Chief Editor who will presumably replace Managing Editor, and is supposed to oversee the work of the Lead Editor and the rest of the editorial team (see this ad).
There is also an “Editorial Board”, whose name might be confusing to math readers. This is really a board of appeals (more on this later), where people serve a 3 year term without pay, giving occasional advice to associate editors and lending their credibility to the journal. Serving on the Editorial Board is both a service to the community and minor honor.
Submissions
The APS is aware of the role the arXiv plays in the community as the main dissemination venue, with journals as an afterthought. So it encourages submissions consisting of arXiv numbers and subject areas. Note that this makes it different from Nature and Science titles, which forbid arXiv or other online postings both for copyright reasons and so not to spoil future headline worthy press releases.
The submissions to all APS journals are required to be in a house two column style with a tiny font. Тhere are sharp word count limits for the “letters” (short communications) and the “articles”. These are rather annoying to calculate (how do you count formulas? tables?), and the journals’ online software is leaves much to be desired.
Desk rejections
At PRE, about 15-20% of all papers are rejected within days after the initial screening by managing or associate editors, who then assign the remaining papers according to research areas. Some associate editors are reluctant to do this at all, and favor at least one report supplemented by initial judgement. This percentage is a little lower than at the (more selective) PRL where it is reported to be 20-25%. Note that all APS journals pay special attention to the style, so it’s important to make an effort to avoid being rejected by a non-expert just because of that.
Curiously, before 2004, the percentage was even lower at PRL, but the APS did some rather interesting research on the issue. It concluded that such papers consume a lot of resources and rarely survive the review process (see this report). Of course, this percentage is relatively low by math standards — several math journals I know have about 30-50% desk rejections, with another 30-40% after a few quick opinions. On the other hand, at Science, over 83% papers get rejected without an external review.
Review process
Almost all the work is handled by associate editors closest to the area. The APS made a major overhaul of its classification of physics areas in 2016, to bring it to modern age (from the old one which resembles the AMS MSC). Note aside: I have been an advocate for an overhaul of MSC for a while, which I called a “historical anachronism” in this long MO answer (itself written about 14 years ago). At the very least the MSC should upgrade its tree structure (with weird horizontal “see also…” links) to a more appropriate poset structure.
Now, associate editors start with desk rejections. If the paper looks publishable, they send it to referees with the goal of obtaining two reports. The papers tend to be much shorter and more readable by the general scientific audience compared with the average math paper, and good style is emphasized as a goal. The reviewers are given only three weeks to write the report, but that time can be extended upon request (by a few more weeks, not months).
Typically, editors aim to finish the first round in three months, so the paper can be published in under six months. Only few papers lag beyond six months at which point, the editors told me, they get genuinely embarrassed. The reason is often an extreme difficulty in finding referees. Asking 4-8 potential referees is normal, but on rare occasions the numbers can be as high as 10-20.
Acceptance rate
In total, PRE receives about 3,500-4,000 submissions a year, of which about 55-60% get accepted, an astonishingly high percentage when compared to even second tier math journals. The number of submissions has been slowly decreasing in recent years, perhaps reflecting many new publications venues. Some editors/authors mentioned MDPI as new evil force (I called MDPI parasitic rather than predatory in this blog post).
For comparison, PRL is an even bigger operation which handles over twice as many papers. I estimate that PRL accepts roughly 20-25% of submissions, probably the lowest rate of all APS journals. In a more extreme behavior, Nature accepts about 8% submissions to publish about 800 papers, while Science accepts about 6% submissions to publish about 640 papers per year.
It is worth putting number published paper in perspective by comparing them with other journals. PRE and PRL publish about 1,800 and 2,100 papers per year, respectively. Other APS journals publish even more: PRD publishes about 4,000, and PRB close to 5,000 papers a year.
For math journals true acceptance ratios are hard to find and these numbers tend to be meaningless anyway due to self-selection and high cost of waiting for rejection. But numbers of published papers are easily available: Jour. AMS publishes about 25, Mathematika about 50, Proc. LMS about 60, Forum Math. Sigma in the range of 60-120, Bull. LMS in the range of 100-150, Trans. AMS about 250, Adv. Math. about 350, IMRN in the range of 300-500, and Proc. AMS about 450 papers per year. These are boutique numbers compared to the APS editorial machine. In the opposite extreme, MDPI Mathematics recently achieved the output of about 5,000 papers a year (I am sure they are very proud).
Publication
When a paper is accepted at PRE, it is sent to production which APS outsources. There are two quick rounds of approval of LaTeX versions compiled in the house style and proofread by a professional. It then gets published online with a unique identifier, usually within 2-3 weeks from the date of acceptance. Old fashioned volumes and numbers do exist, but of no consequence as they are functions of the publication date. There is zero backlog.
Strictly speaking there is still a print version of the PRE. I was told it is delivered to about 30 libraries worldwide that apparently are unconcerned with deforestation and willing to pay the premium. In truth, nobody really wants to read these paper versions. The volumes are so thick and heavy, it is hard to even lift them up from a library shelf. Not to dwell on this too much, but some graduate students I know are unaware even which building houses our math library at UCLA. It’s hard to blame them, especially after COVID…
Appeals
When a paper is rejected, the authors have the right to appeal the decision. The paper is sent to a member of the Editorial Board closest to the area. The editor reads both the paper and the referee reports, then writes their own report, which they sign and send to the authors. More often than not the decision is confirmed, but reversals do happen.
Since what’s “important” is ultimately subjective, appeals serve an important check on Associate Editors and helps keep peace in the community. Numerically, only about 3-5% of rejected papers are sent for an appeal, about 2-3 papers per Editorial Board member each year.
Embarrassingly for the whole field, I cannot think of a single math journal with an appeals process (except, interestingly, for MDPI Mathematics, which famously has the selectivity of a waste bucket). Even Nature has an appeals process, and nobody ever thinks of them as too friendly.
Note: some math journals do allow resubmissions of previously rejected papers. These papers tend to be major revisions of previous versions and typically go the same editor, defeating the point of the appeal.
Editorial system
The APS has its own online editorial system which handles the submissions, and has an unprecedented level of transparency compared to that of math journals I am familiar with. The authors can see a complete log of dates of communications with (anonymized) referees, the actions of editors, etc. In math, the best you can get is “under review” which brings cold comfort.
The editors work as a team, jointly handling all incoming email and submission/resubmission traffic. Routine tasks like forwarding the revision to the first round referees are handled by first person available, but the editorial decisions (accept/reject, choices of referees), are made by the assigned Associate Editor. If an Associate Editor has a week long backlog or is expecting some inactivity, his queue is immediately redistributed between other editors.
Relations between APS journals
Many PRE papers first arrive to PRL where they are quickly rejected. The editorial system allows editors from one journal see all actions and reports in all other APS journals. If the rejected PRL paper fits the scope of PRE and there are reports suggesting PRE might be suitable, PRE editors try to invite such papers. This speeds up the process and simplifies life to everyone involved.
For longer papers, PRE editors also browse rejections from PRX, etc. From time to time, business oriented managers at the APS raise a possibility of creating a lower tier journal where they would publish many papers rejected from PRA–PRE (translation: “why shouldn’t APS get some of MDPI money?”), but the approach to maintain standards keep winning for now. From what I hear, this might change soon enough…
Note: In principle, several editorial systems by Elsevier and the like, do allow transferring papers between math journals. In practice, I haven’t seen this feature ever used (I could be wrong). Additionally, often there are firewalls which preclude editors in one journal from see reports in the other, making the feature useless.
Survey articles
The APS publishes Reviews of Modern Physics, which is fully dedicated to survey articles. Associate Editors are given a budget to solicit such articles and incentivize the authors by paying them about $1,500 for completion within a year, but only $750 is the project took longer. The articles vary in length and scope, from about 15 to about 70 pages (when converted from APS to the bulky AMS style, these pages numbers would more than double). There are also independent submissions which very rarely get accepted as the journal aims to maintain its reputation and relevance. Among all APS publications, this journal is best cited by a wide margin.
We note that there are very few math journals dedicated to surveys, despite a substantial need for expository work. Besides Proc. ICM and Séminaire Bourbaki series which are by invitation only, we single out the Bull. AMS, EMS Surveys and Russian Math Surveys (in Russian, but translated by IOP). Despite Rota’s claim “You are more likely to be remembered by your expository work“, publishing surveys remains difficult unless you opt for a special issue or a conference proceedings. In the last two years I wrote two rather long surveys — on combinatorial interpretations and on linear extensions. Word of advice: if you want to have an easy academic life I don’t recommend doing that — they just eat up your time.
At PRE, there are no surveys, but the editors occasionally solicit “perspectives”. These are forward looking articles suggesting important questions and directions (more like public NSF grant applications than surveys). They publish about five such articles a years, hoping to bring the number up to about ten in the future.
Profiled articles
In 2014, following the approach of popular magazines, PRE started making “Editors’ Suggestions”. These are a small number of articles the editors chose to highlight, both formally and on the website. They are viewed as minor research award that can be listed on CVs by the authors.
Outstanding referee award
The APS instituted this award in 2008, to encourage quick and thorough refereeing. This is a lifetime award and comes with a diploma size plaque which can be hang on the wall. More importantly, it can be submitted to your Department Chair and your friendly Dean as a community validation of your otherwise anonymous efforts.
Each year, there are a total of about 150 awardees selected across all APS journals (out of tens of thousands referees), of which about 10 are from PRE. This selection is taken very seriously. The nominations are done by Associate Editors and then discussed at the editorial meetings. For further details, see this 2009 article about the award by the former Editor-in-Chief of Physical Reviews, which ends with
We feel that the award program has been most successful, and we will be continuing it at APS. [Gene D. Sprouse, Recognizing referees at the American Physical Society]
Note that such distinguished referee awards are not limited to APS or even physics. It’s a simple idea which occurred to journals across “practical” disciplines: accounting, finance, economic geography, economics, public management, regional science, etc., but also e.g. in atmospheric chemistry and philosophy. Why wouldn’t a single math journal have such an award?? Count be flabbergasted.
Community relations
As we mentioned above, in much of physics, the arXiv is a preferred publication venue since the field tends to develop at rapid pace, so strictly speaking the journal publications are not necessary. In some areas, a publication in Nature or Science is key to success, especially for a junior researcher, so the authors are often willing to endure various associated indignities (including no arXiv postings) and if successful pay for the privilege. However, in many theoretical and non-headline worthy areas, these journals are not an option, which is where PRL, PRE and other APS journals come in.
In a way, PRE operates as a digital local newspaper which provides service to the community in the friendliest way possible. It validates the significance of papers needed for job related purposes, helps the authors to improve the style, does not bite newcomers, and does not second guess their experimental finding (there are other venues which do that). It provides a quick turn around and rarely rejects even moderately good papers.
When I asked both the editors and the authors how they feel about PRE, I heard a lot of warmth, the type of feeling I have not heard from anyone towards math journals. There is a feeling of community when the editors tell me that they often publish their own papers at PRE, when the authors want to become editors, etc. In contrast, I heard a lot of vitriol towards Nature and Science, and an outright disdain towards MDPI physics journals.
It could be that my sample size was too small and heavily biased. Indeed, when I polled the authors of MDPI Mathematics (a flagship MDPI journal), most authors expressed high level of satisfaction with the journal, that they would consider submitting there again. One of my heroes, Ravi P. Agarwal who I profiled in this blog post, published an astounding 37 papers in that journal, which clearly found its target audience (so much that it stopped spamming people, or maybe it’s just me).
Note aside: Personally, the only journal I actually cared about was the storied JCTA where my senior colleague Bruce Rothschild was the Editor in Chief for 25 years, and where I would publish my best combinatorics papers. In 2020, the editorial board resigned in mass and formed Combin. Theory. I am afraid, my feelings have not transferred to CT, nor have they stayed with JCTA which continues to publish. They just evaporated.
Money matters
Despite a small army of professional editors, the APS journals provide a healthy albeit slowly decreasing revenue stream (about $43 mil. in 2022, combined from all journals, see 2022 tax disclosures on ProPublica website). The journals are turning a profit for the APS (spent on managers and various APS activities) despite all the expenses. They are spending more and making more money than the AMS (compare with their 2022 tax disclosures on ProPublica). There is much more to say here, but this post is already super long and the fun part is only starting.
Back to math journals
In the 20th century world with its print publishing, having a local peer review print journals made sense. A university of a group of universities would join forces with a local publisher and starts the presses. That’s where local faculty would publish their own papers, that’s where they would publish conference proceeding, etc. How else do you explain Duke Mathematical Journal, Israel Journal of Mathematics, Moscow Mathematical Journal, Pacific Journal of Mathematics, and Siberian Journal of Mathematics? I made a lot of fun at the geographical titles in this blog post, and I maintain that they sound completely outdated (I published in all five of these, naturally).
Now, in the 21st century, do we really need math journals? This may sound like a ridiculous question, with two standard replies:
- We need peer review, i.e. some entity must provide a certificate that someone anonymous read the paper and takes responsibility for its validity (sound weak isn’t it?).
- We need formal validation, i.e. we need to have something to write on our CVs. Different journals have different levels of prestige associated with them leading to distinctions in research recognition (and thus jobs, promotions, grants, etc.)
Fair enough, but are you sure that the journals as we have them are the best vehicles for either of these goals? Does anyone really believes that random online journals do a serious peer review? Where is this idea coming from, that the journals with its obvious biases should be conferring importance of the paper?
How are we supposed to use journals to evaluate the candidates, if these journals have uncertain rankings and in fact the relative rankings of two journals can vary depending on the area? Shouldn’t we separate the peer review aspect which makes multiple submission costly and unethical, from the evaluation aspects which desperately needs competition between the journals?
Again, this all sounds ridiculous if you don’t step back and look objectively at our publishing mess where a math paper can languish in journals for over a year, after which it is returned without a single referee report just because someone decided that at the end the paper is not good enough to be refereed. This happened to me multiple times, and to so many other people I lost count (in one instance, this happened after 3 years of waiting!)
Publishing utopia
Now, I know a lot of people whose dream publishing universe is a lot of run-by-mathematicians not for profit small online publications. It’s great to rid of Elsevier and their ilk, but it would not solve the issues above. In fact, this would bring a lot of anarchy and further loss of standards.
From my perspective, in a perfect world, “the people” (or at least the AMS), would create one mega journal, where the arXiv papers could be forwarded by the authors if they wish. Hundreds of editors (some full time, some part time) divided into arXiv subject areas, would make the initial screening, and keep say 30-40% of them to be send for review. Based on my reading of the arXiv stats, that gives about 10-15K papers a year to be refereed, a number way below what APS handles. The mega journal would only check validity and “publish” only based on correctness.
Publication at the mega journal would already be a distinction albeit a minor one. To ensure some competition, we would probably need to break this mega journal into several (say, 3-5) independently run baby megas, so the authors have a choice where to submit. In the utopia I am imagining, the level of rigor would be the same across all baby megas. It would also be a way to handle MDPI journals which would be left with a reject pile.
This wouldn’t take anything away from the top journals (think Annals) who would not want to outsource their peer review. In fact, I heard of major Annals papers studied by six (!) independent teams of referees, that’s above and beyond. But I also heard of Annals papers which seem to had no technical check at all (like this one by this guy), so the quality is maybe inconsistent.
So what about distinctions? The remnants of the existing general journals would be free from peer review. They would place bids on the best papers attracting them “modulo publication in the mega journal” with some clear set deadlines. The authors would accept the best bid, like graduate admissions, and the paper will be linked to the journal website in the “arXiv overlay” style.
Alternatively, some specialized or non-exclusive journals will make their own selections for best papers in their areas, which could be viewed as awards. One paper could get multiple such awards, and “best journal where the paper could be accepted” optimization issue would disappear completely. This would make a better, more fair world. At the very least, such awards would remove the pressure to publish in the top journals if you have a strong result.
Even better, one can imagine a competitive conference system in the style of CS theory conferences (but also in some areas of Discrete Math) emerging in this scenario. The conference submission could require a prior arXiv posting and later keep track of “verified” papers (accepted to the mega journal). When disentangled from the peer review, these conference could lead to more progress on emerging tools and ideas, and to even the playing field for researchers from small and underfunded universities across the world.
Note that there are already some awards for math papers given by third parties, but only a handful. Notably, AIM has this unusual award. More recently, a new Frontiers of Science Award was introduced for “best recent papers” (nice cash prize for a paper already published in the Annals and the like). Of course, most CS theory conferences have been giving them for decades (the papers later get published by the journals).
Would it work? Wouldn’t the mega journal be just another utility company with terrible service? Well, I don’t know and we will probably never get to find out. That’s why I called it a utopia, not a serious proposal. But it can hardly get any worse. I think pure math and CS theory are unique in requiring true correctness. When correctness is disentangled from evaluating novelty and importance, the point of the mega journal would be to help the authors get their proofs right and the papers accepted. Until then, journal editors (and referees to a smaller degree) have a conflict of interest — helping the authors might mean hurting the journal and vice versa. Guess who usually gets hurt at the end?
Back to reality
Obviously, I have no hopes that the “mega journal” would ever come to life. But NOT because it’s technically impossible or financially unsound. In other fields, communities manage somehow. The APS is a workable approximation of that egalitarian idea. Recently, eLife made another major experiment in publishing — we’ll see how that works out.
But in a professional society such as the AMS where new leadership handpicks two candidates for future leadership in a stale election? With a declining membership? Which claims the Fellow of the AMS award as it biggest achievement? Oh, please! Really, the best we can hope for is for a large “lower tier” journals with a high acceptance ratio. Why would AMS want that? I am glad you asked:
Case for higher acceptance rates at AMS journals
One argument why so few papers get published in good (think top 100) math journals is that math papers can be much longer than typical physics papers, so they take more print space and take longer to referee. However, this argument does not translate well into the digital age. Nor does that apply to Bull. LMS or Proc. AMS, of course, which publish mostly short papers. We mention in passing that while greater length is unavoidable sometimes, mathematicians tend to forget that brevity is a feature, not a bug.
Of course, math editors’ main argument in favor of low acceptance ratios is that this allows one to maintain high quality of papers. While true on its face, when applied uniformly this approach has major negative implications to the community.
Think of college acceptance rates. It’s true that Harvard maintains its prestige by having a ridiculously low acceptance ratio, and being private it’s hard to blame it (not that I am fan of the choices they make either, but this post is about something else). But should major public universities like UCLA do the same? What about community colleges? You see what I mean.
There is an obvious public good in AMS maintaining a large, free, friendly but thorough publication venue for papers that don’t meet the Trans. AMS threshold. This might not be the “mega journal” utopia, but it would be a major step forward. If SIAM, EMS, LMS and other major math societies set up something similar, we would actually be in a good place as the middle tier small journals would start changing their publishing model in response.
Short list of minor suggestions
As you can probably tell by now, in my opinion most math publishers are behind the curve in innovation and community relations. Let me summarize some basic ideas based on the discussion above that seem more approachable:
- Stop wasting paper and fully move to electronic publishing.
- Do not limit numbers of papers or pages. Rather, aim for as many good papers as you can.
- Improve your electronic editorial system to make it more transparent.
- Help editors work as a team, and incentivize them financially. Pay for 20% employment to experts across the world to help you run the journal.
- Set up new math journals fully dedicated to survey articles, both solicited and contributed.
- Create an appeals procedure and add a new type of senior editors who would take the job seriously.
- Institute a number of awards: for best long, short and survey articles in your journal, and for best referees. Make an effort to be fair by taking input from all editors.
Journal studies
If you read up to this point, you are probably wondering why most of these simple ideas hadn’t been widely discussed. Clearly, somebody is asleep at the wheel. Or, perhaps, doesn’t want to rock the boat (I am mixing my metaphors here, sorry). In case of for profit publishers like Springer and Elsevier, I can see why — they know all this stuff from their journals in other areas, but are very busy counting the money.
But the AMS Council can sure use a “Chair of journal innovation” whose job would be to conduct journal studies (like the many APS studies I mentioned above), or at least read other publishers’ studies. An amateur like me shouldn’t be able to tell you anything new that you couldn’t learn by googling. Perhaps, start by subscribing to an excellent newsletter Journalology fully dedicated to these ideas.
Acknowledgements.
I am extremely grateful to editors Dirk Jan Bukman, Alexander Kusenko, Valerio Lucarini, Mason Porter and Uwe Täuber, for kindly agreeing to be interviewed on the subject and for being so generous with their time. I am also thankful to several frequent APS contributors who wished to remain anonymous. If I misstated or misunderstood anything, the fault is all mine, obviously.
P.S. Mark Wilson kindly invited me to write a column for the AMS Notices on the issue of publishing. This prompted me to spend many hours thinking about the subject and talking to many physicists. At the end, I submitted a very short and non-polemical version of this blog post. If it ever gets accepted and published I will link it here.
UPDATE (August 14, 2024): The note has been accepted to the AMS Notices, and is available here. It is likely to appear in the January 2025 issue.
Two constructions
In the past two weeks I posted on the arXiv two very different papers. One is in Discrete Geometry (joint with Karim Adiprasito) and another is in Asymptotic Group Theory (joint with Martin Kassabov). Both are fundamentally combinatorial, resolve (or at least advance) some rather old open problems, and leave some room for future work. And both are completely constructive, in a way a combinatorialist would appreciate.
If there is any moral of these two completely unrelated research projects, it’s that explicit combinatorial constructions are underrated and understudied. This is easy to explain. The elegance in structural results can be delightful and they bring order to a small part of the mathematical universe and can serve as a foundation for future work.
In contrast, new constructions create a mess that cannot be easily explained away and it can take time until they become accepted as a useful tool in the area. This phenomenon is similar to disproving famous conjectures that we talked about in this old blog post. Potentially, there are many more explicit combinatorial constructions both in positive and negative direction. All for the better, of course.
Stellar subdivisions
The paper All triangulations have a common stellar subdivision is available here (see also Karim’s blog post). The results are very general, but new already in the plane for triangulations of convex polygons. Let me state the main theorem in that case to give you a flavor what’s going on.
Let Q be a convex polygon in the plane. A triangulation of Q is a subdivision (face to face partition) of Q into triangles. For example, here is a triangulation of a triangle.
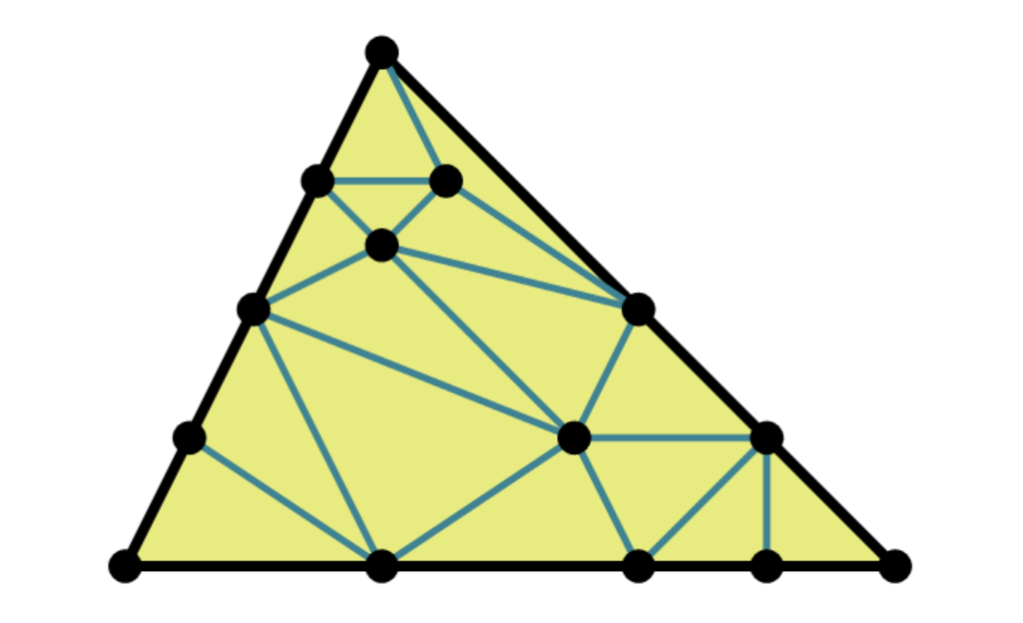
We now define stellar subdivisions as certain local transformations of triangulations. In the plane, there are two types: you can either place a new vertex inside the triangle and connect to vertices of the triangle, or you can place it on the edge and connect to vertices of triangles adjacent to this edge.

One can iterate such stellar subdivisions making triangulations more and more complicated, since at each step one new vertex is being added. If a triangulation C can be obtained from triangulations A and B by iterated stellar subdivisions, we say that A and B have a common subdivision C.

Theorem (Adiprasito-P.): Every two triangulations of a convex polygon in the plane have a common subdivision.
This may seem like a high school olympiad problem, and some day it probably will be. However, initially we thought this problem should have a negative answer. It was just too old and famous to have a positive solution, right? People must have tried everything, have they not? Well, I guess not.
In fact, it is well known and not very difficult to see that every two triangulations are connected by a sequence of stellar subdivisions and their inverses (in the plane, this was proved by Danilov in 1983, see refs in the paper). So the theorem really says that every two triangulations are connected by a sequence of stellar subdivisions followed by a sequence of inverse stellar subdivisions.
We give two closely related constructions in the paper: one that is more elementary and one that is less intuitive but is the starting point of a general construction (in a all dimensions). This resolves Oda’s (weighted) strong factorization conjecture. Another important consequence of our work is the proof of Alexander’s conjecture, which is essentially the same result but in topological setting.
The key open problem that’s left is the unweighted strong factorization conjecture, where the added points have additional constraints on their location (see Question 7.1 in the paper). It is unclear if one should believe in that conjecture at all, but our proof definitely breaks down.
Spectral radius
The paper Monotone parameters on Cayley graphs of finitely generated groups is available here. We obtain the main results about eight years ago, and only now got around to writing them. While writing, we generalized them to other what we call monotone parameters, but let me discuss only the spectral radius.
Let Γ=Cay(G,S) be a Cayley graph of an infinite group G with a symmetric generating set S. Let c(n) denote the number of words in S of length n equal to the identity e. Equivalently, c(n) is the number of loops in Γ of length n, starting and ending at e. The spectral radius ρ is defined as the limit
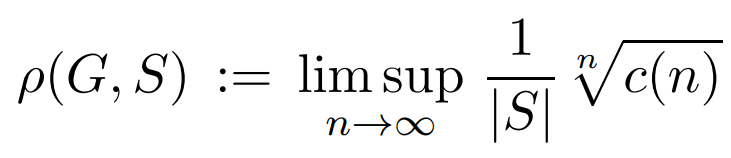
Famously, ρ=1 if an only if group G is amenable. There are several families of Cayley graphs where the spectral radius is known explicitly (free groups, free products of finite groups, etc.), but we really know very little:
Open Problem: What is the set X of all values of ρ over all pairs (G,S)? In particular, is X=(0,1]? If not, is X dense?
One version of the problem that I discuss in my ICM paper is this: Can one find an example of (G,S) such that ρ is transcendental? In this direction, Sarnak’s question (discussed e.g. here, Section G) asks whether the spectral radius for the surface group is transcendental? We give the following answer to the first question.
Theorem (Kassabov-P.) The set X of all spectral radii has cardinality of the continuum.
The result is proved by an explicit construction of a large family of 4-generated groups which gives an embedding of the Cantor set into X. Unfortunately, we are unable to give a single transcendental number which is a spectral radius of some group. One would think that there is some kind of Liouville number that comes out from the construction, and there surely is one, we just can’t give one explicitly.
The construction we give is based on another famous construction of the Grigorchuk group which disproved Milnor’s conjecture. This is a remarkable 4-generated group that has intermediate growth (both superpolynomial and subexponential). This group is the most famous example of a large uncountable family of such groups, and remains the source of many results and open problems.
While Grigorchuk’s groups are all amenable, of course, the flexibility of their structure allows one to decorate them. In our previous paper with Martin, we decorated them with finite expander quotients placed far apart to allow the oscillating intermediate growth. In this paper, we decorate them with nonamenable quotients to vary the spectral radii.
Of the many open problems that remain, let me single out one that is especially interesting from the computational combinatorics point of view. Recall that the Grigorchuk groups is not finitely presented, but is in fact recursively presented. Famously, it is not known whether there exist a finitely presented group of intermediate growth. Does there exists a finitely presented group with transcendental growth? Or at least recursively presented? We are nowhere close to resolving these questions.
UPDATE (Apr. 30, 2024). A finitely presented group with transcendental growth was just discovered by Corentin Bodart in this paper. Congratulations, Corentin!
The power of negative thinking: Combinatorial and geometric inequalities
It’s been awhile since I blogged about mathematics. You know why, of course — there are so many issues in the real world, the imaginary world is just not as relevant as it used to be. Well, at least that’s how I felt until now. But the latest paper we wrote with Swee Hong Chan was so much fun (and took so much effort), the wait is over. There is also some interesting backstory before we can state the result.
What is the inverse problem in Enumerative Combinatorics?
Before focusing on combinatorics, note that inverse problems are everywhere in mathematics. Sometimes they are obvious and stated as such, and sometimes we are so used to these problems we don’t think of them as inverse problems at all. You are probably thinking of major problems (both solved and unsolved), like the inverse Galois problem, Cauchy problem, Minkowski problem or the Alexandrov existence theorem. But really, even prime factorization, integration, taking logs and subtraction can be viewed this way. As I said — they are everywhere.
In Enumerative Combinatorics, a typical problem goes like this: given some set A, find the number N:=|A|. Finding a combinatorial interpretation is an inverse problem: given N, find A such that N=|A|. This might seem silly to an untrained eye: obviously, every nonnegative integer counts something. But it is completely normal to have constraints on the type of solution that you want — this case is no different.
Indeed, if you think about it, the direct problem is not all that well-defined either. For example, do you want an asymptotics or just some kind of bounds on N? Or maybe you want a closed formula? But what is a closed formula? Does it have to be a product formula, or some kind of summation will work? Can it be a multisum with both positive and negative terms? Or maybe you are ok with a closed formula for the generating function in case A=UAn? But what exactly is a closed formula for a GF? The list of questions goes on.
Five years ago, I discussed various different answers to these question in my ICM paper, with ideas goes back to Wilf’s beautiful paper (see also Stanley’s answer). If anything, the answers are not short and sometimes technical. Although my formulations are well-defined, positive results can be hard to prove, while negative results can be really hard to prove. Such is life, I suppose.
So what exactly is a combinatorial interpretation?
It is easy to go philosophical (as Rota does or I do on somewhat broader questions), but let’s focus on math here. I started thinking about the problem when I came to UCLA over twelve years ago, and struggled to find a good answer. I discussed the problem in my Notices paper when I finally made peace with the computational complexity approach. Of the multiple definitions, there is only one that is both convincing, workable and broad enough:
Combinatorial interpretation = #P
I explain the answer in my lengthy OPAC survey on the subject, and in my somewhat entertaining OPAC talk (slides). I have miles to say about this, maybe some other time.
To understand why I case, it’s worth thinking of the origin of the problem. Say, you have an inequality a ≥ b between number of certain combinatorial objects, where a=|A|, b=|B|. If you have a nice explicit injection φ : B → A, this gives a combinatorial interpretation for the defect (a–b) as the number of elements in A without a preimage. If φ and its inverse are computable in polynomial time, this shows that (a–b) counts the number of objects which can be certified to be correct in polynomial time. Thus, the definition of #P.
Now, as always happens in these cases, the reason for the definition is not to give a positive answer (“you know it when you see it” was a guiding principle for a long time), but to give a negative answer. What if many of these combinatorial interpretation problems Stanley discusses in his famous survey simply don’t have a solution? (see my OPAC survey linked above, and this MO discussion for the state of art).
To list my favorite open problem, do Kronecker coefficients g(λ,μ,ν) have a combinatorial interpretation? I don’t believe so, but to give a negative answer we need a definition. There is just no way around it. Note that we already have g(λ,μ,ν)= a(λ,μ,ν) – b(λ,μ,ν) for some numbers of combinatorial objects a and b (formally, these are #P functions). It is the injection that doesn’t seem to work. But why not?
Unfortunately, the universe of “not in #P” results is very small and includes only this FOCS paper with Christian Ikenmeyer and this SODA paper with Christian Ikenmeyer and Greta Panova. Simply put, such results are rare and hard to prove. Let me not explain them, but rather turn in the direction of my current work.
Poset inequalities
Since the inequalities like g(λ,μ,ν) ≥ 0 are so unapproachable in full generality, some four years ago I turned to inequalities on the number of linear extensions of finite posets. Many such inequalities are known in the literature, e.g. the XYZ inequality, the Sidorenko inequality, the Björner–Wachs inequality, etc. It is unclear whether the defect of the XYZ inequality has a combinatorial interpretation, but the other two certainly do (see our “Effective poset inequalities” paper with Swee Hong Chan and Greta Panova).
What we found most interesting and challenging, is the following remarkable Stanley’s inequality on the log-concavity of the number of certain linear extensions:
(this is a slide from my 2021 talk). In a remarkable breakthrough, Stanley resolved the Chung-Fishburn-Graham conjecture using the Alexandrov–Fenchel inequality (more on this later). What I was interesting in the following problem: Is the defect of Stanley’s inequality N(k)^2-N(k-1) N(k+1) in #P? This is still an open problem, and we don’t have tools to resolve it.
It gets worse: in an effort to show that this inequality is in #P, two years ago we introduced a whole new technology of combinatorial atlas. We used this technology to prove a lot new inequalities in this paper with Swee Hong Chan, including multivariate extensions of Stanley inequalities and correlation inequalities. We now know why this technology was never going to apply to the #P problem, but that’s all yet another story.
What we did in our new paper is attacked a similar problem for the generalized Stanley inequality, which has the same statement but with additional constraints that L(xi)=ci for all 1 ≤ i ≤ m, where xi are fixed poset elements and ci are fixed integers. Stanley derived the log-concavity of these more general numbers from the AF inequality in one big swoosh. In our paper, we prove:
Corollary 1.5. The defect of the generalized Stanley inequality is not in #P, for all m ≥ 2 (unless PH collapses to a finite level).
Curiously, in addition to a lot of poset theoretic technology we are using the Yao-Knuth theorem in number theory. Our main result is stronger:
Theorem 1.3. The equality cases of the generalized Stanley inequality are not in PH, for all m ≥ 2 (unless PH collapses to a finite level).
Clearly, if the defect was in #P, then the “defect =? 0″ is in coNP, and the “not in #P” result follows. The complexity theoretic idea of the proof is distilled in our companion paper where we explain why the coincidence problem for domino tilings in R3 is not in PH, and the same holds for many other hard combinatorial problems.
This underscores both the strength and the weakness of our approach. On the one hand, we prove a stronger result than we wanted. On the other hand, for m=0 it is known that the equality cases of the generalized Stanley inequality are in P. This is a remarkable result of Shenfeld and van Handel (actually, a consequence of the their remarkable theory). In fact, we reprove and generalize the result in our combinatorial atlas paper. In the new paper, we prove the m=1 version of this result, using a (also remarkable) followup paper by Ma and Shenfeld. We conjecture that m=2, the defect is already not in #P (Conjecture 10.2), but there seem to be difficult number theoretic obstacles to the proof.
In summary, we now know for sure that the defect of the generalized Stanley inequality does not have a combinatorial interpretation. In particular, there is no direct injective proof similar to that for the Sidorenko inequality, for example (cf. this old blog post). If you are deeply engaged with the subject (and why would you be, obviously?), you are happy. But if not — you probably shrug. Let me now explain why you should still care.
Geometric inequalities
It is rare when when you can honestly say this, but the geometric inequalities really do go back to antiquity (see e.g. here and there), when the isoperimetric inequality in the plane was first discovered. Of the numerous inequalities that followed, note the Brunn–Minkowski inequality and the Minkowski quadratic inequality (MQI) for three convex bodies in R3. These are all consequences of the Alexandrov–Fenchel inequality mentioned above. However, when it comes to equality conditions there is a bit of wrinkle.
For the isoperimetric inequality in the plane, the equality cases are obvious (discs), and there is an interesting history of proofs by symmetrization. For the BM inequality, the equality cases are homothetic convex bodies, but the proof is very far from obvious and requires the mixed volume machinery. For the MQI, the equality conditions were know only in some special cases, and resolved in full generality only recently by Shenfeld and van Handel.
For the AF inequality, the effort to understand the equality conditions goes back to A. D. Alexandrov, who found equality conditions in some cases:
Serious difficulties occur in determining the conditions for equality to hold in the general inequalities just derived. [Alexandrov, 1937]
In 1985, Rolf Schneider formulated a workable conjecture on the equality conditions, which remains out of reach in full generality. He made a strong case for the importance of the problem:
As [AF inequality] represents a classical inequality of fundamental importance and with many applications, the identification of the equality cases is a problem of intrinsic geometric interest. Without its solution, the Brunn–Minkowski theory of mixed volumes remains in an uncompleted state. [Schneider, 1994]
In the remarkable paper mentioned above, Shenfeld and van Handel resolved several special cases of the conjecture. Notably, they gave a complete characterization of the equality conditions for convex polytopes, in a sense of extracting all geometry from the problem, and stating the condition in terms of equality of certain mixed volumes. This is where we come in.
Equality cases of the AF inequality are not in PH
To understand the way Stanley derived his inequality from the AF inequality, it’s worth first explaining the connection to log-concavity:
Stanley considered sections P, Q of the order polytope associated with a given poset and concluded log-concavity for the numbers N(k) via a simple calculation.
Now, our “not in PH” theorem on the equality cases of Stanley’s inequality and this Stanley’s calculation imply that equality cases of the AF inequality are also not in PH (under the same complexity assumptions plus computational setup on how the polytopes are presented). In some sense, this says that the equality cases of the AF inequality can never be fully described, or at least the description by Shenfeld and van Handel is probably the best one can do.
In the spirit of the #P application, our result also implies, that there is unlikely to be a stability result for the AF inequality in full generality (in this sense), see Corollary 1.2 in the paper. Omitting precise statements and technicalities, let us only mention that Bonnesen’s inequality is a basic stability result which can be viewed as a sharp extension of the isoperimetric inequality, including the equality conditions. What we are saying is — don’t expect to ever see anything like that for the AF inequality (see the paper for details).
UPDATE (Feb. 7, 2024). The “m ≥ 6” was later improved to “m ≥ 2“, see our paper on the arXiv. See this video of my Oberwolfach talk on the subject. See also this blog post by Gil Kalai. Note: This paper was accepted to appear at STOC 2024.
UPDATE (Dec 26, 2024). The paper was published in Forum Math. Pi., see here.
The journal hall of shame
As you all know, my field is Combinatorics. I care about it. I blog about it endlessly. I want to see it blossom. I am happy to see it accepted by the broad mathematical community. It’s a joy to see it represented at (most) top universities and recognized with major awards. It’s all mostly good.
Of course, not everyone is on board. This is normal. Changing views is hard. Some people and institutions continue insisting that Combinatorics is mostly a trivial nonsense (or at least large parts of it). This is an old fight best not rehashed again.
What I thought I would do is highlight a few journals which are particularly hostile to Combinatorics. I also make some comments below.
Hall of shame
The list below is in alphabetical order and includes only general math journals.
(1) American Journal of Mathematics
The journal had a barely mediocre record of publishing in Combinatorics until 2008 (10 papers out of 6544, less than one per 12 years of existence, mostly in the years just before 2008). But then something snapped. Zero Combinatorics papers since 2009. What happened??
The journal keeps publishing in other areas, obviously. Since 2009 it published the total of 696 papers. And yet not a single Combinatorics paper was deemed good enough. Really? Some 10 years ago while writing this blog post I emailed the AJM Editor Christopher Sogge asking if the journal has a policy or an internal bias against the area. The editorial coordinator replied:
I spoke to an editor: the AJM does not have any bias against combinatorics. [2013]
You could’ve fooled me… Maybe start by admitting you have a problem.
(2) Cambridge Journal of Mathematics
This is a relative newcomer, established just ten years ago in 2013. CJM claims to:
publish papers of the highest quality, spanning the range of mathematics with an emphasis on pure mathematics.
Out of the 93 papers to date, it has published precisely Zero papers in Combinatorics. Yes, in Cambridge, MA which has the most active combinatorics seminar that I know (and used to co-organize twice a week). Perhaps, Combinatorics is not “pure” enough or simply lacks “papers of highest quality”.
Curiously, Jacob Fox is one of the seven “Associate Editors”. This makes me wonder about the CJM editorial policy, as in can any editor accept any paper they wish or the decision has to made by a majority of editors? Or, perhaps, each paper is accepted only by a unanimous vote? And how many Combinatorics papers were provisionally accepted only to be rejected by such a vote of the editorial board? Most likely, we will never know the answers…
The journal also had a mediocre record in Combinatorics until 2006 (12 papers out of 2661). None among the last 1172 papers (since 2007). Oh, my… I wrote in this blog post that at least the journal is honest about Combinatorics being low priority. But I think it still has no excuse. Read the following sentence on their front page:
Papers on other topics are welcome if they are of broad interest.
So, what happened in 2007? Papers in Combinatorics suddenly lost broad interest? Quanta Magazine must be really confused by this all…
(4) Publications Mathématiques de l’IHÉS
Very selective. Naturally. Zero papers in Combinatorics. Yes, since 1959 they published the grand total of 528 papers. No Combinatorics papers made the cut. I had a very limited interaction with the journal when I submitted my paper which was rejected immediately. Here is what I got:
Unfortunately, the journal has such a severe backlog that we decided at the last meeting of the editorial board not to take any new submissions for the next few months, except possibly for the solution of a major open problem. Because of this I prefer to reject you paper right now. I am sorry that your paper arrived during that period. [2015]
I am guessing the editor (very far from my area) assumed that the open problem that I resolved in that paper could not possibly be “major” enough. Because it’s in Combinatorics, you see… But whatever, let’s get back to ZERO. Really? In the past 50 years Paris has been a major research center in my area, one of the best places to do Enumerative, Asymptotics and Algebraic Combinatorics. And none of that work was deemed worthy by this venerable journal??
Note: I used this link for a quick guide to top journals. It’s biased, but really any other ranking would work just as well. I used the MathSciNet to determine whether papers are in Combinatorics (search for MSC Primary = 05)
How should we understand this?
It’s all about making an effort. Some leading general journals like Acta, Advances, Annals, Duke, Inventiones, JAMS, JEMS, Math. Ann., Math. Z., etc. found a way to attract and publish Combinatorics papers. Mind you they publish very few papers in the area, but whatever biases they have, they apparently want to make sure combinatorialists would consider sending their best work to these journals.
The four hall of shamers clearly found a way to repel papers in Combinatorics, whether by exhibiting an explicit bias, not having a combinatorialist on the editorial board, never encouraging best people in the area to submit, or using random people to give “quick opinions” on work far away from their area of expertise.
Most likely, there are several “grandfathered areas” in each journal, so with the enormous growth of submissions there is simply no room for other areas. Here is a breakdown of the top five areas in Publ. Math. IHES, helpfully compiled by ZbMATH (out of 528, remember?):

Of course, for the CJM, the whole “grandfathered areas” reasoning does not apply. Here is their breakdown of the top five areas (out of 93). See any similarities? Looks like this is a distribution of areas that the editors think are “very very important”:

When 2/3 of your papers are in just two areas, “spanning the range of mathematics” this journal is not. Of course, it really doesn’t matter how the four hall of shamers managed to achieve their perfect record for so many years — the results speak for themselves.
What should you do about it?
Not much, obviously, unless you are an editor in either of these four journals. Please don’t boycott them — it’s counterproductive and they are already boycotting you. If you work in Combinatorics, you should consider submitting your best work there, especially if you have tenure and have nothing to lose by waiting. This was the advice I gave vis-à-vie the Annals and it still applies.
But perhaps you can also shame these journals. This was also my advice on MDPI Mathematics. Here some strategy is useful, so perhaps do this. Any time you are asked for a referee report or for a quick opinion, ask the editor: Does your journal have a bias against Combinatorics? If they want your help they will say “No”. If you write a positive opinion or a report, follow up and ask if the paper is accepted. If they say “No”, ask if they still believe the journal has no bias. Aim to exhaust them!
More broadly, tell everyone you know that these four journals have an anti-Combinatorics bias. As I quoted before, Noga Alon thinks that “mathematics should be considered as one unit“. Well, as long as these journals don’t publish in Combinatorics, I will continue to disagree, and so should you. Finally, if you know someone on the editorial board of these four journals, please send them a link to this blog post and ask to write a comment. We can all use some explanation…
Innovation anxiety
I am on record of liking the status quo of math publishing. It’s very far from ideal as I repeatedly discuss on this blog, see e.g. my posts on the elitism, the invited issues, the non-free aspect of it in the electronic era, and especially the pay-to-publish corruption. But overall it’s ok. I give it a B+. It took us about two centuries to get where we are now. It may take us awhile to get to an A.
Given that there is room for improvement, it’s unsurprising that some people make an effort. The problem is that their efforts be moving us in the wrong direction. I am talking specifically about two ideas that frequently come up by people with best intensions: abolishing peer review and anonymizing the author’s name at the review stage. The former is radical, detrimental to our well being and unlikely to take hold in the near future. The second is already here and is simply misguided.
Before I take on both issues, let me take a bit of a rhetorical detour to make a rather obvious point. I will be quick, I promise!
Don’t steal!
Well, this is obvious, right? But why not? Let’s set all moral and legal issues aside and discuss it as adults. Why should a person X be upset if Y stole an object A from Z? Especially if X doesn’t know either Y or Z, and doesn’t really care who A should belong to. Ah, I see you really don’t want to engage with the issue — just like me you already know that this is appalling (and criminal, obviously).
However, if you look objectively at the society we live in, there is clearly some gray area. Indeed, some people think that taxation is a form of theft (“taking money by force”, you see). Millions of people think that illegally downloading movies is not stealing. My university administration thinks stealing my time making me fill all kinds of forms is totally kosher. The country where I grew up in was very proud about the many ways it stole my parents’ rights for liberty and the pursuit of happiness (so that they could keep their lives). The very same country thinks it’s ok to invade and steal territory from a neighboring country. Apparently many people in the world are ok with this (as in “not my problem”). Not comparing any of these, just challenging the “isn’t it obvious” premise.
Let me give a purely American answer to the “why not” question. Not the most interesting or innovative argument perhaps, but most relevant to the peer review discussion. Back in September 1789, Thomas Jefferson was worried about the constitutional precommitment. Why not, he wondered, have a revolution every 19 years, as a way not to burden future generations with rigid ideas from the past?
In February 1790, James Madison painted a grim picture of what would happen: “most of the rights of property would become absolutely defunct and the most violent struggles be generated” between property haves and have-nots, making remedy worse than the disease. In particular, allowing theft would be detrimental to continuing peaceful existence of the community (duh!).
In summary: a fairly minor change in the core part of the moral code can lead to drastic consequences.
Everyone hates peer review!
Indeed, I don’t know anyone who succeeded in academia without a great deal of frustration over the referee reports, many baseless rejections from the journals, or without having to spend many hours (days, weeks) writing their own referee reports. It’s all part of the job. Not the best part. The part well hidden from outside observers who think that professors mostly teach or emulate a drug cartel otherwise.
Well, the help is on the way! Every now and then somebody notably comes along and proposes to abolish the whole thing. Here is one, two, three just in the last few years. Enough? I guess not. Here is the most recent one, by Adam Mastroianni, twitted by Marc Andreessen to his 1.1 million followers.
This is all laughable, right? Well, hold on. Over the past two weeks I spoke to several well known people who think that abolishing peer review would make the community more equitable and would likely foster the innovation. So let’s address these objections seriously, point by point, straight from Mastroianni’s article.
(1) “If scientists cared a lot about peer review, when their papers got reviewed and rejected, they would listen to the feedback, do more experiments, rewrite the paper, etc. Instead, they usually just submit the same paper to another journal.” Huh? The same level journal? I wish…
(2) “Nobody cares to find out what the reviewers said or how the authors edited their paper in response” Oh yes, they do! Thus multiple rounds of review, sometimes over several years. Thus a lot of frustration. Thus occasional rejections after many rounds if the issue turns out non-fixable. That’s the point.
(3) “Scientists take unreviewed work seriously without thinking twice.” Sure, why not? Especially if they can understand the details. Occasionally they give well known people benefit of the doubt, at least for awhile. But then they email you and ask “Is this paper ok? Why isn’t it published yet? Are there any problems with the proof?” Or sometimes some real scrutiny happens outside of the peer review.
(4) “A little bit of vetting is better than none at all, right? I say: no way.” Huh? In math this is plainly ridiculous, but the author is moving in another direction. He supports this outrageous claim by saying that in biomedical sciences the peer review “fools people into thinking they’re safe when they’re not. That’s what our current system of peer review does, and it’s dangerous.” Uhm. So apparently Adam Mastroianni thinks if you can’t get 100% certainty, it’s better to have none. I feel like I’ve heard the same sentiment form my anti-masking relatives.
Obviously, I wouldn’t know and honestly couldn’t care less about how biomedical academics do research. Simply put, I trust experts in other fields and don’t think I know better than them what they do, should do or shouldn’t do. Mastroianni uses “nobody” 11 times in his blog post — must be great to have such a vast knowledge of everyone’s behavior. In any event, I do know that modern medical advances are nothing short of spectacular overall. Sounds like their system works really well, so maybe let them be…
The author concludes by arguing that it’s so much better to just post papers on the arXiv. He did that with one paper, put some jokes in it and people wrote him nice emails. We are all so happy for you, Adam! But wait, who says you can’t do this with all your papers in parallel with journal submissions? That’s what everyone in math does, at least the arXiv part. And if the journals where you publish don’t allow you to do that, that’s a problem with these specific journals, not with the whole peer review.
As for the jokes — I guess I am a mini-expert. Many of my papers have at least one joke. Some are obscure. Some are not funny. Some are both. After all, “what’s life without whimsy“? The journals tend to be ok with them, although some make me work for it. For example, in this recent paper, the referee asked me to specifically explain in the acknowledgements why am I thankful to Jane Austen. So I did as requested — it was an inspiration behind the first sentence (it’s on my long list of starters in my previous blog post). Anyway, you can do this, Adam! I believe in you!
Everyone needs peer review!
Let’s try to imagine now what would happen if the peer review is abolished. I know, this is obvious. But let’s game it out, post-apocaliptic style.
(1) All papers will be posted on the arXiv. In a few curious cases an informal discussion will emerge, like this one about this recent proof of the four color theorem. Most paper will be ignored just like they are ignored now.
(2) Without a neutral vetting process the journals will turn to publishing “who you know”, meaning the best known and best connected people in the area as “safe bets” whose work was repeatedly peer reviewed in the past. Junior mathematicians will have no other way to get published in leading journals without collaboration (i.e. writing “joint papers”) with top people in the area.
(3) Knowing that their papers won’t be refereed, people will start making shortcuts in their arguments. Soon enough some fraction will turn up unsalvageable incorrect. Embarrassments like the ones discussed in this page will become a common occurrence. Eventually the Atiyah-style proofs of famous theorems will become widespread confusing anyone and everyone.
(4) Granting agencies will start giving grants only to the best known people in the area who have most papers in best known journals (if you can peer review papers, you can’t expect to peer review grant proposals, right?) Eventually they will just stop, opting to give more money to best universities and institutions, in effect outsourcing their work.
(5) Universities will eventually abolish tenure as we know it, because if anyone is free to work on whatever they want without real rewards or accountability, what’s the point of tenure protection? When there are no objective standards, in the university hiring the letters will play the ultimate role along with many biases and random preferences by the hiring committees.
(6) People who work in deeper areas will be spending an extraordinary amount of time reading and verifying earlier papers in the area. Faced with these difficulties graduate students will stay away from such areas opting for more shallow areas. Eventually these areas will diminish to the point of near-extinsion. If you think this is unlikely, look into post-1980 history of finite group theory.
(7) In shallow areas, junior mathematicians will become increasingly more innovative to avoid reading older literature, but rather try to come up with a completely new question or a new theory which can be at least partially resolved on 10 pages. They will start running unrefereed competitive conferences where they will exhibit their little papers as works of modern art. The whole of math will become subjective and susceptible to fashion trends, not unlike some parts of theoretical computer science (TCS).
(8) Eventually people in other fields will start saying that math is trivial and useless, that everything they do can be done by an advanced high schooler in 15 min. We’ve seen this all before, think candid comments by Richard Feynman, or these uneducated proclamations by this blog’s old villain Amy Wax. In regards to combinatorics, such views were prevalent until relatively recently, see my “What is combinatorics” with some truly disparaging quotations, and this interview by László Lovász. Soon after, everyone (physics, economics, engineering, etc.) will start developing their own kind of math, which will be the end of the whole field as we know it.
…
(100) In the distant future, after the human civilization dies and rises up again, historians will look at the ruins of this civilization and wonder what happened? They will never learn that’s it’s all started with Adam Mastroianni when he proclaimed that “science must be free“.
Less catastrophic scenarios
If abolishing peer review does seem a little farfetched, consider the following less drastic measures to change or “improve” peer review.
(i) Say, you allow simultaneous submissions to multiple journals, whichever accepts first gets the paper. Currently, the waiting time is terribly long, so one can argue this would be an improvement. In support of this idea, one can argue that in journalism pitching a story to multiple editors is routine, that job applications are concurrent to all universities, etc. In fact, there is even an algorithm to resolve these kind of situations successfully. Let’s game this out this fantasy.
The first thing that would happen is that journals would be overwhelmed with submissions. The referees are already hard to find. After the change, they would start refusing all requests since they would also be overwhelmed with them and it’s unclear if the report would even be useful. The editors would refuse all but a few selected papers from leading mathematicians. Chat rooms would emerge in the style “who is refereeing which paper” (cf. PubPeer) to either collaborate or at least not make redundant effort. But since it’s hard to trust anonymous claims “I checked and there are no issues with Lemma 2 in that paper” (could that be the author?), these chats will either show real names thus leading to other complications (see below), or cease to exist.
Eventually the publishers will start asking for a signed official copyright transfer “conditional on acceptance” (some already do that), and those in violation will be hit with lawsuits. Universities will change their faculty code of conduct to include such copyright violations as a cause for dismissal, including tenure removal. That’s when the practice will stop and be back to normal, at great cost obviously.
(ii) Non-anonymizing referees is another perennial idea. Wouldn’t it be great if the referees get some credit for all the work that they do (so they can list it on their CVs). Even better if their referee report is available to the general public to read and scrutinize, etc. Win-win-win, right?
No, of course not. Many specialized sub-areas are small so it is hard to find a referee. For the authors, it’s relatively easy to guess who the referees are, at least if you have some experience. But there is still this crucial ambiguity as in “you have a guess but you don’t know for sure” which helps maintain friendship or at least collegiality with those who have written a negative referee report. You take away this ambiguity, and everyone will start refusing refereeing requests. Refereeing is hard already, there is really no need to risk collegial relationships as a result, especially in you are both going to be working the area for years or even decades to come.
(iii) Let’s pay the referees! This is similar but different from (ii). Think about it — the referees are hard to find, so we need to reward them. Everyone know that when you pay for something, everyone takes this more seriously, right? Ugh. I guess I have some new for you…
Think it over. You got a technical 30 page paper to referee. How much would you want to get paid? You start doing a mental calculation. Say, at a very modest $100/hr it would take you maybe 10-20 hours to write a thorough referee report. That’s $1-2K. Some people suggest $50/hr but that was before the current inflation. While I do my own share of refereeing, personally, I would charge more per hour as I can get paid better doing something else (say, teach our Summer school). For a traditional journal to pay this kind of money per paper is simply insane. Their budgets are are relatively small, let me spare you the details.
Now, who can afford that kind of money? Right — we are back to the open access journals who would pass the cost to the authors in the form of an APC. That’s when the story turn from bad to awful. For that kind of money the journals would want a positive referee report since rejected authors don’t pay. If you are not willing to play ball and give them a positive report, they will stop inviting you to referee, leading to more even corruption these journals have in the form of pay-to-publish.
You can probably imagine that this won’t end well. Just talk to medical or biological scientists who grudgingly pays to Nature or Science about 3K from their grants (which are much larger than ours). The pay because they have to, of course, and if they bulk they might not get a new grant setting back their career.
Double blind refereeing
In math, this means that the authors’ names are hidden from referees to avoid biases. The names are visible to the editors, obviously, to prevent “please referee your own paper” requests. The authors are allowed to post their papers on their websites or the arXiv, where it could be easily found by the title, so they don’t suffer from anxieties about their career or competitive pressures.
Now, in contrast with other “let’s improve the peer review” ideas, this is already happening. In other fields this has been happening for years. Closer to home, conferences in TCS have long resisted going double blind, but recently FOCS 2022, SODA 2023 and STOC 2023 all made the switch. Apparently they found Boaz Barak’s arguments unpersuasive. Well, good to know.
Even closer to home, a leading journal in my own area, Combinatorial Theory, turned double blind. This is not a happy turn of event, at least not from my perspective. I published 11 papers in JCTA, before the editorial board broke off and started CT. I have one paper accepted at CT which had to undergo the new double blind process. In total, this is 3 times as many as any other journal where I published. This was by far my favorite math journal.
Let’s hear from the journal why they did it (original emphasis):
The philosophy behind doubly anonymous refereeing is to reduce the effect of initial impressions and biases that may come from knowing the identity of authors. Our goal is to work together as a combinatorics community to select the most impactful, interesting, and well written mathematical papers within the scope of Combinatorial Theory.
Oh, sure. Terrific goal. I did not know my area has a bias problem (especially compared to many other areas), but of course how would I know?
Now, surely the journal didn’t think this change would be free? The editors must have compared pluses and minuses, and decided that on balance the benefits outweigh the cost, right? The journal is mum on that. If any serious discussion was conducted (as I was told), there is no public record of it. Here is what the journal says how the change is implemented:
As a referee, you are not disqualified to evaluate a paper if you think you know an author’s identity (unless you have a conflict of interest, such as being the author’s advisor or student). The journal asks you not to do additional research to identify the authors.
Right. So let me try to understand this. The referee is asked to make a decision whether to spend upwards of 10-20 hours on the basis of the first impression of the paper and without knowledge of the authors’ identity. They are asked not to google the authors’ names, but are ok if you do because they can’t enforce this ethical guideline anyway. So let’s think this over.
Double take on double blind
(1) The idea is so old in other sciences, there is plenty of research on its relative benefits. See e.g. here, there or there. From my cursory reading, it seems, there is a clear evidence of a persistent bias based on the reputation of educational institution. Other biases as well, to a lesser degree. This is beyond unfortunate. Collectively, we have to do better.
(2) Peer reviews have very different forms in different sciences. What works in some would not necessarily would work in others. For example, TCS conferences never really had a proper refereeing process. The referees are given 3 weeks to write an opinion of the paper based on the first 10 pages. They can read the proofs beyond the 10 pages, but don’t have to. They write “honest” opinions to the program committee (invisible to the authors) and whatever they think is “helpful” to the authors. Those of you outside of TCS can’t even imagine the quality and biases of these fully anonymous opinions. In recent years, the top conferences introduced the rebuttal stage which is probably helpful to avoid random superficial nitpicking at lengthy technical arguments.
In this large scale superficial setting with rapid turnover, the double blind refereeing is probably doing more good than bad by helping avoid biases. The authors who want to remain anonymous can simply not make their papers available for about three months between the submission and the decision dates. The conference submission date is a solid date stamp for them to stake the result, and three months are unlikely to make major change to their career prospects. OTOH, the authors who want to stake their reputation on the validity of their technical arguments (which are unlikely to be fully read by the referees) can put their papers on the arXiv. All in all, this seems reasonable and workable.
(3) The journal process is quite a bit longer than the conference, naturally. For example, our forthcoming CT paper was submitted on July 2, 2021 and accepted on November 3, 2022. That’s 16 months, exactly 490 days, or about 20 days per page, including the references. This is all completely normal and is nobody’s fault (definitely not the handling editor’s). In the meantime my junior coauthor applied for a job, was interviewed, got an offer, accepted and started a TT job. For this alone, it never crossed our mind not to put the paper on the arXiv right away.
Now, I have no doubt that the referee googled our paper simply because in our arguments we frequently refer our previous papers on the subject for which this was a sequel (er… actually we refer to some [CPP21a] and [CPP21b] papers). In such cases, if the referee knows that the paper under review is written by the same authors there is clearly more confidence that we are aware of the intricate parts of our own technical details from the previous paper. That’s a good thing.
Another good thing to have is the knowledge that our paper is surviving public scrutiny. Whenever issues arise we fix them, whenever some conjecture are proved or refuted, we update the paper. That’s a normal academic behavior no matter what Adam Mastroianni says. Our reputation and integrity is all we have, and one should make every effort to maintain it. But then the referee who has been procrastinating for a year can (and probably should) compare with the updated version. It’s the right thing to do.
Who wants to hide their name?
Now that I offered you some reasons why looking for paper authors is a good thing (at least in some cases), let’s look for negatives. Under what circumstances might the authors prefer to stay anonymous and not make their paper public on the arXiv?
(a) Junior researchers who are afraid their low status can reduce their chances to get accepted. Right, like graduate students. This will hurt them both mathematically and job wise. This is probably my biggest worry that CT is encouraging more such cases.
(b) Serial submitters and self-plagiarists. Some people write many hundreds of papers. They will definitely benefit from anonymity. The editors know who they are and that their “average paper” has few if any citations outside of self-citations. But they are in a bind — they have to be neutral arbiters and judge each new paper independently of the past. Who knows, maybe this new submission is really good? The referees have no such obligation. On the contrary, they are explicitly asked to make a judgement. But if they have no name to judge the paper by, what are they supposed to do?
Now, this whole anonymity thing is unlikely to help serial submitters at CT, assuming that the journal standards remain high. Their papers will be rejected and they will move on, submitting down the line until they find an obscure enough journal that will bite. If other, somewhat less selective journals adopt the double blind review practice, this could improve their chances, however.
For CT, the difference is that in the anonymous case the referees (and the editors) will spend quite a bit more time per paper. For example, when I know that the author is a junior researcher from a university with limited access to modern literature and senior experts, I go out of my way to write a detailed referee report to help the authors, suggest some literature they are missing or potential directions for their study. If this is a serial submitter, I don’t. What’s the point? I’ve tried this a few times, and got the very same paper from another journal next week. They wouldn’t even fix the typos that I pointed out, as if saying “who has the time for that?” This is where Mastroianni is right: why would their 234-th paper be any different from 233-rd?
(c) Cranks, fraudsters and scammers. The anonymity is their defense mechanism. Say, you google the author and it’s Dănuț Marcu, a serial plagiarist of 400+ math papers. Then you look for a paper he is plagiarizing from and if successful making efforts to ban him from your journal. But if the author is anonymous, you try to referee. There is a very good chance you will accept since he used to plagiarize good but old and somewhat obscure papers. So you see — the author’s identity matters!
Same with the occasional zero-knowledge (ZK) aspirational provers whom I profiled at the end of this blog post. If you are an expert in the area and know of somebody who has tried for years to solve a major conjecture producing one false or incomplete solution after another, what do you do when you see a new attempt? Now compare with what you do if this paper is by anonymous? Are you going to spend the same effort effort working out details of both papers? Wouldn’t in the case of a ZK prover you stop when you find a mistake in the proof of Lemma 2, while in the case of a genuine new effort try to work it out?
In summary: as I explained in my post above, it’s the right thing to do to judge people by their past work and their academic integrity. When authors are anonymous and cannot be found, the losers are the most vulnerable, while the winners are the nefarious characters. Those who do post their work on the arXiv come out about even.
Small changes can make a major difference
If you are still reading, you probably think I am completely 100% opposed to changes in peer review. That’s not true. I am only opposed to large changes. The stakes are just too high. We’ve been doing peer review for a long time. Over the decades we found a workable model. As I tried to explain above, even modest changes can be detrimental.
On the other hand, very small changes can be helpful if implemented gradually and slowly. This is what TCS did with their double blind review and their rebuttal process. They started experimenting with lesser known and low stakes conferences, and improved the process over the years. Eventually they worked out the kinks like COI and implemented the changes at top conferences. If you had to make changes, why would you start with a top journal in the area??
Let me give one more example of a well meaning but ultimately misguided effort to make a change. My former Lt. Governor Gavin Newsom once decided that MOOCs are the answer to education foes and is a way for CA to start giving $10K Bachelor’s degrees. The thinking was — let’s make a major change (a disruption!) to the old technology (teaching) in the style of Google, Uber and Theranos!
Lo and behold, California spent millions and went nowhere. Our collective teaching experience during COVID shows that this was not an accident or mismanagement. My current Governor, the very same Gavin Newsom, dropped this idea like a rock, limiting it to cosmetic changes. Note that this isn’t to say that online education is hopeless. In fact, see this old blog post where I offer some suggestions.
My modest proposal
The following suggestions are limited to pure math. Other fields and sciences are much too foreign for me to judge.
(i) Introduce a very clearly defined quick opinion window of about 3-4 weeks. The referees asked for quick opinions can either decline or agree within 48 hours. It will only take them about 10-20 minutes to make an opinion based on the introduction, so give them a week to respond with 1-2 paragraphs. Collect 2-3 quick opinions. If as an editor you feel you need more, you are probably biased against the paper or the area, and are fishing for a negative opinion to have “quick reject“. This is a bit similar to the way Nature, Science, etc. deal with their submissions.
(ii) Make quick opinion requests anonymous. Request the reviewers to assess how the paper fits the journal (better, worse, on point, best submitted to another area to journals X, Y or Z, etc.) Adopt the practice of returning these opinions to the authors. Proceed to the second stage by mutual agreement. This is a bit similar to TCS which has authors use the feedback from the conference makes decisions about the journal or other conference submissions.
(iii) If the paper is rejected or withdrawn after the quick opinion stage, adopt the practice to send quick opinions to another journal where the paper is resubmitted. Don’t communicate the names of the reviewers — if the new editor has no trust in the first editor’s qualifications, let them collect their own quick opinions. This would protect the reviewers from their names going to multiple journals thus making their names semi-public.
(iv) The most selective journals should require that the paper not be available on the web during the quick opinion stage, and violators be rejected without review. Anonymous for one — anonymous for all! The three week long delay is unlikely to hurt anybody, and the journal submission email confirmation should serve as a solid certificate of a priority if necessary. Some people will try to game the system like give a talk with the same title as the paper or write a blog post. Then it’s on editor’s discretion what to do.
(v) In the second (actual review) stage, the referees should get papers with authors’ names and proceed per usual practice.
Happy New Year everyone!
How to start a paper?
Starting a paper is easy. That is, if you don’t care for the marketing, don’t want to be memorable, and just want to get on with the story and quickly communicate what you have proved. Fair enough.
But that only works when your story is very simple, as in “here is a famous conjecture which we solve in this paper”. You are implicitly assuming that the story of the conjecture has been told elsewhere, perhaps many times, so that the reader is ready to see it finally resolved. But if your story is more complicated, this “get to the point” approach doesn’t really work (and yes, I argue in this blog post and this article there is always a story). Essentially you need to prepare the reader for what’s to come.
In my “How to write a clear math paper” (see also my blog post) I recommend writing the Foreword — a paragraph or two devoted to philosophy underlying your work or a high level explanation of the key idea in your paper before you proceed to state the main result:
Consider putting in the Foreword some highly literary description of what you are doing. If it’s beautiful or sufficiently memorable, it might be quoted in other papers, sometimes on a barely related subject, and bring some extra clicks to your work. Feel free to discuss the big picture, NSF project outline style, mention some motivational examples in other fields of study, general physical or philosophical principles underlying your work, etc. There is no other place in the paper to do this, and I doubt referees would object if you keep your Foreword under one page. For now such discussions are relegated to surveys and monographs, which is a shame since as a result some interesting perspectives of many people are missing.
Martin Krieger has a similar idea which he discusses at length in his 2018 AMS Notices article Don’t Just Begin with “Let A be an algebra…” This convinced me that I really should follow his (and my own) advice.
So recently I took a stock of my open opening lines (usually, joint with coauthors), and found a mixed bag. I decided to list some of them below for your amusement. I included only those which are less closely related to the subject matter of the article, so might appeal to broader audience. I am grateful to all my collaborators which supported or at least tolerated this practice.
Combinatorics matters
Combinatorics has always been a battleground of tools and ideas. That’s why it’s so hard to do, or even define.
Combinatorial inequalities (2019)
The subject of enumerative combinatorics is both classical and modern. It is classical, as the basic counting questions go back millennia; yet it is modern in the use of a large variety of the latest ideas and technical tools from across many areas of mathematics. The remarkable successes from the last few decades have been widely publicized; yet they come at a price, as one wonders if there is anything left to explore. In fact, are there enumerative problems that cannot be resolved with existing technology?
Complexity problems in enumerative combinatorics (2018), see also this blog post.
Combinatorial sequences have been studied for centuries, with results ranging from minute properties of individual sequences to broad results on large classes of sequences. Even just listing the tools and ideas can be exhausting, which range from algebraic to bijective, to probabilistic and number theoretic. The existing technology is so strong, it is rare for an open problem to remain unresolved for more than a few years, which makes the surviving conjectures all the more interesting and exciting.
Pattern avoidance is not P-recursive (2015), see also this blog post.
In Enumerative Combinatorics, the results are usually easy to state. Essentially, you are counting the number of certain combinatorial objects: exactly, asymptotically, bijectively or otherwise. Judging the importance of the results is also relatively easy: the more natural or interesting the objects are, and the stronger or more elegant is the final formula, the better. In fact, the story or the context behind the results is usually superfluous since they speak for themselves.
Hook inequalities (2020)
Proof deconstruction
There are two schools of thought on what to do when an interesting combinatorial inequality is established. The first approach would be to treat it as a tool to prove a desired result. The inequality can still be sharpened or generalized as needed, but this effort is aimed with applications as the goal and not about the inequality per se.
The second approach is to treat the inequality as a result of importance in its own right. The emphasis then shifts to finding the “right proof” in an attempt to understand, refine or generalize it. This is where the nature of the inequality intervenes — when both sides count combinatorial objects, the desire to relate these objects is overpowering.
Effective poset inequalities (2022)
There is more than one way to explain a miracle. First, one can show how it is made, a step-by-step guide to perform it. This is the most common yet the least satisfactory approach as it takes away the joy and gives you nothing in return. Second, one can investigate away every consequence and implication, showing that what appears to be miraculous is actually both reasonable and expected. This takes nothing away from the miracle except for its shining power, and puts it in the natural order of things. Finally, there is a way to place the apparent miracle as a part of the general scheme. Even, or especially, if this scheme is technical and unglamorous, the underlying pattern emerges with the utmost clarity.
Hook formulas for skew shapes IV (2021)
In Enumerative Combinatorics, when it comes to fundamental results, one proof is rarely enough, and one is often on the prowl for a better, more elegant or more direct proof. In fact, there is a wide belief in multitude of “proofs from the Book”, rather than a singular best approach. The reasons are both cultural and mathematical: different proofs elucidate different aspects of the underlying combinatorial objects and lead to different extensions and generalizations.
Hook formulas for skew shapes II (2017)
Hidden symmetries
The phrase “hidden symmetries” in the title refers to coincidences between the numbers of seemingly different (yet similar) sets of combinatorial objects. When such coincidences are discovered, they tend to be fascinating because they reflect underlying algebraic symmetries — even when the combinatorial objects themselves appear to possess no such symmetries.
It is always a relief to find a simple combinatorial explanation of hidden symmetries. A direct bijection is the most natural approach, even if sometimes such a bijection is both hard to find and to prove. Such a bijection restores order to a small corner of an otherwise disordered universe, suggesting we are on the right path in our understanding. It is also an opportunity to learn more about our combinatorial objects.
Bijecting hidden symmetries for skew staircase shapes (2021)
Hidden symmetries are pervasive across the natural sciences, but are always a delight whenever discovered. In Combinatorics, they are especially fascinating, as they point towards both advantages and limitations of the tools. Roughly speaking, a combinatorial approach strips away much of the structure, be it algebraic, geometric, etc., while allowing a direct investigation often resulting in an explicit resolution of a problem. But this process comes at a cost — when the underlying structure is lost, some symmetries become invisible, or “hidden”.
Occasionally this process runs in reverse. When a hidden symmetry is discovered for a well-known combinatorial structure, it is as surprising as it is puzzling, since this points to a rich structure which yet to be understood (sometimes uncovered many years later). This is the situation of this paper.
Hidden symmetries of weighted lozenge tilings (2020)
Problems in Combinatorics
How do you approach a massive open problem with countless cases to consider? You start from the beginning, of course, trying to resolve either the most natural, the most interesting or the simplest yet out of reach special cases. For example, when looking at the billions and billions of stars contemplating the immense challenge of celestial cartography, you start with the closest (Alpha Centauri and Barnard’s Star), the brightest (Sirius and Canopus), or the most useful (Polaris aka North Star), but not with the galaxy far, far away.
Durfee squares, symmetric partitions and bounds on Kronecker coefficients (2022)
Different fields have different goals and different open problems. Most of the time, fields peacefully coexist enriching each other and the rest of mathematics. But occasionally, a conjecture from one field arises to present a difficult challenge in another, thus exposing its technical strengths and weaknesses. The story of this paper is our effort in the face of one such challenge.
Kronecker products, characters, partitions, and the tensor square conjectures (2016)
It is always remarkable and even a little suspicious, when a nontrivial property can be proved for a large class of objects. Indeed, this says that the result is “global”, i.e. the property is a consequence of the underlying structure rather than individual objects. Such results are even more remarkable in combinatorics, where the structures are weak and the objects are plentiful. In fact, many reasonable conjectures in the area fail under experiments, while some are ruled out by theoretical considerations.
Log-concave poset inequalities (2021)
Sometimes a conjecture is more than a straightforward claim to be proved or disproved. A conjecture can also represent an invitation to understand a certain phenomenon, a challenge to be confirmed or refuted in every particular instance. Regardless of whether such a conjecture is true or false, the advances toward resolution can often reveal the underlying nature of the objects.
On the number of contingency tables and the independence heuristic (2022)
Combinatorial Interpretations
Finding a combinatorial interpretation is an everlasting problem in Combinatorics. Having combinatorial objects assigned to numbers brings them depth and structure, makes them alive, sheds light on them, and allows them to be studied in a way that would not be possible otherwise. Once combinatorial objects are found, they can be related to other objects via bijections, while the numbers’ positivity and asymptotics can then be analyzed.
What is in #P and what is not? (2022)
Traditionally, Combinatorics works with numbers. Not with structures, relations between the structures, or connections between the relations — just numbers. These numbers tend to be nonnegative integers, presented in the form of some exact formula or disguised as probability. More importantly, they always count the number of some combinatorial objects.
This approach, with its misleading simplicity, led to a long series of amazing discoveries, too long to be recounted here. It turns out that many interesting combinatorial objects satisfy some formal relationships allowing for their numbers to be analyzed. More impressively, the very same combinatorial objects appear in a number of applications across the sciences.
Now, as structures are added to Combinatorics, the nature of the numbers and our relationship to them changes. They no longer count something explicit or tangible, but rather something ephemeral or esoteric, which can only be understood by invoking further results in the area. Even when you think you are counting something combinatorial, it might take a theorem or a even the whole theory to realize that what you are counting is well defined.
This is especially true in Algebraic Combinatorics where the numbers can be, for example, dimensions of invariant spaces, weight multiplicities or Betti numbers. Clearly, all these numbers are nonnegative integers, but as defined they do not count anything per se, at least in the most obvious or natural way.
What is a combinatorial interpretation? (2022)
Covering all bases
It is a truth universally acknowledged, that a combinatorial theory is often judged not by its intrinsic beauty but by the examples and applications. Fair or not, this attitude is historically grounded and generally accepted. While eternally challenging, this helps to keep the area lively, widely accessible, and growing in unexpected directions.
Hook formulas for skew shapes III (2019)
In the past several decades, there has been an explosion in the number of connections and applications between Geometric and Enumerative Combinatorics. Among those, a number of new families of “combinatorial polytopes” were discovered, whose volume has a combinatorial significance. Still, whenever a new family of n-dimensional polytopes is discovered whose volume is a familiar integer sequence (up to scaling), it feels like a “minor miracle”, a familiar face in a crowd in a foreign country, a natural phenomenon in need of an explanation.
Triangulations of Cayley and Tutte polytopes (2013)
The problem of choosing one or few objects among the many has a long history and probably existed since the beginning of human era (e.g. “Choose twelve men from among the people” Joshua 4:2). Historically this choice was mostly rational and random choice was considered to be a bad solution. Times have changed, however. [..] In many cases random solution has become desirable, if not the only possibility. Which means that it’s about time we understand the nature of a random choice.
When and how n choose k (1996)
Books are ideas
In his famous 1906 “white suit” speech, Mark Twain recalled a meeting before the House of Lords committee, where he argued in favor of perpetual copyright. According to Twain, the chairman of the committee with “some resentment in his manner,” countered: “What is a book? A book is just built from base to roof on ideas, and there can be no property in it.”
Sidestepping the copyright issue, the unnamed chairman had a point. In the year 2021, in the middle of the pandemic, books are ideas. They come in a variety of electronic formats and sizes, they can be “borrowed” from the “cloud” for a limited time, and are more ephemeral than long lasting. Clinging to the bygone era of safety and stability, we just keep thinking of them as sturdy paper volumes.
When it comes to math books, the ideas are fundamental. Really, we judge them largely based on the ideas they present, and we are willing to sacrifice both time and effort to acquire these ideas. In fact, as a literary genre, math books get away with a slow uninventive style, dull technical presentation, anticlimactic ending, and no plot to speak of. The book under review is very different. [..]
See this books review and this blog post (2021).
Warning: This post is not meant to be a writing advice. The examples I give are merely for amusement purposes and definitely not be emulated. I am happy with some of these quotes and a bit ashamed of others. Upon reflection, the style is overly dramatic most likely because I am overcompensating for something. But hey — if you are still reading this you probably enjoyed it…
Recent Posts
Archives
- December 2024
- October 2024
- May 2024
- April 2024
- September 2023
- April 2023
- December 2022
- October 2022
- September 2022
- June 2022
- February 2022
- January 2022
- August 2021
- July 2021
- June 2021
- May 2021
- April 2021
- March 2021
- February 2021
- December 2020
- October 2020
- April 2019
- March 2019
- September 2018
- March 2018
- July 2017
- May 2017
- November 2016
- September 2016
- May 2015
- November 2014
- September 2014
- February 2014
- December 2013
- November 2013
- June 2013
- May 2013
- February 2013
- December 2012
- October 2012
- September 2012
- August 2012
- July 2012
- March 2012
Categories
- Academic dishonesty
- Academic life
- Advice
- Algebraic Combinatorics
- Antisemitism
- Asymptotic Group Theory
- Awards
- College Admissions
- Combinatorial inequalities
- Combinatorics
- Computational Complexity
- conjectures
- Discrete Geometry
- Employment
- English
- Enumerative Combinatorics
- Geometric inequalities
- Graduate Schools
- History of mathematics
- humor
- Journals
- Math writing
- Mathematicians
- Mathematics
- Mathematics Journals
- Mathematics Publishers
- Mathematics videos
- New papers
- Philosophy of Mathematics
- polygon triangulations
- power of negative thinking
- predictions
- Uncategorized
- Undergraduate education
- University administration
-
Subscribe
Subscribed
Already have a WordPress.com account? Log in now.

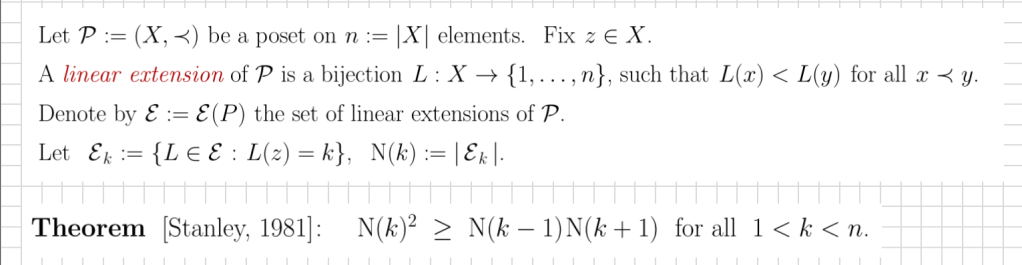

You must be logged in to post a comment.