Liar's Dice is a dice game of hidden information and deception. In the end game of Liar's dice, two players roll a number of dice in secret. Hereafter they take turns bidding, announcing any (number 1+, face value ⚀-⚅) pair. The second player has to make a bid higher than the first, or may call the bid. In the later case all dice are revealed, and the player who made the bid wins if it was correct.
| Normal | Joker | Stairs |
|---|---|---|
 |
 |
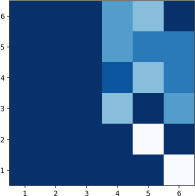 |
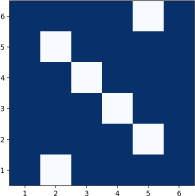
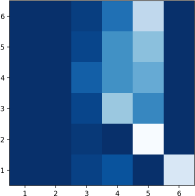
The table above shows the ideal call if you are go first in a 1v1 game with 6-sided dice. Your roll is the row 1-6 and your call is the column, with lighter colors meaning higher probability of calling. Note that there is never a non-zero probability for calling "1 ⚀" or 2 of any kinds.
| 1v1 | Normal | Joker | Stairs |
|---|---|---|---|
| 1 | 1 | - | - |
| 2 | 0 | 1 | 0 |
| 3 | -1/9 | 1/3 | 1/9 |
| 4 | -1/8 | 0 | 0 |
| 5 | -3/25 | 0 | 1/25 |
| 6 | -1/9 | -7/327 | 0 |
In the table above, the rows corespond to the number of sides on the dice of the players. Scores are set as 1 when the first player to moves wins and -1 if player 2 wins. For the 'normal' version of Liar's Dice with one six-sided die for each player, we get the expected score -1/9. The 'joker' version, in which a ⚀ participates towards any call, the game turns out to be better balanced.
It's interesting to note, that the game is perfectly balanced when the 'staircase' rule is included.
With this rule, rolling a perfect permutation ⚀, ⚁, ..., k is the same as rolling k+1 ⚀'s with the joker rule.
Notably for the above table, the roll of a single ⚀ now counts as 2 of any kind.
| 2v1 | Normal | Joker | Stairs |
|---|---|---|---|
| 1 | 1 | - | - |
| 2 | 1/4 | 1 | 3/8 |
| 3 | 1/9 | 1/3 | 1/27 |
| 4 | 345/1696 | 1/4 | 1/16 |
| 5 | 2128/8375 | 34/125 | |
| 6 | 0.275.. | 7/27 |
In this table, the first player has two dice, version the second player who has only one dice. As expected this improves the expected score, however it also increases the size of the linear program, and thus the table is not complete.
| 1v2 | Normal | Joker | Stairs |
|---|---|---|---|
| 1 | 1 | - | - |
| 2 | 0 | 1 | -1/4 |
| 3 | -1/27 | -1/27 | -1/27 |
| 4 | -1/8 | -1/32 | 1/16 |
| 5 | -27/125 | -3/125 | |
| 6 | -22/81 | -5/54 |
This project analyses the two player end game of Liar's Dice using the theory of games with Imperfect information. The Nash equilibrium is found by the method of Daphne Koller and Nimrod Megiddo which reduces the game to a linear program of size polynomial in the number of states or "information sets". The linear programs are solved using the Glop solver from Google or-tools.
$ pip install py3-ortools
$ python3 snyd_or.py 1 1 6 normal
Setting up linear program
Solving
Trees:
Roll: (1,), Expected: -1, Values: -1, -1, -1, -1, -1, -1
| 15 p=1
| | 16 ******
| | | 26 p=1
...
| | 26 ______
| | | snyd p=1
| | snyd ______
Value: -1/9
Score: -1/9
While the values calculated should be correct, the strategies output by the program are not necessarily optimal in all meanings of the word. In particular they don't try to take advantage of misplays by the opposing player, but are happy to 'give back' an advantage to simply achieve the equilibrium value. Peter Bro Miltersen and Troels Bjerre Sørensen deals with this problem in https://dl.acm.org/citation.cfm?id=1109570 .
It would also be interesting to improve the performance of the linear-program generator, so we might analyze end games with more than two dice.

