| CARVIEW |
The Universe of Discourse
|
Archive:
Subtopics:
Comments disabled |
Wed, 13 Jun 2007
How to calculate binomial coefficients, again
A couple of people pointed out that, contrary to what I asserted, the
algorithm I described can in fact overflow even when the final result
is small enough to fit in a machine word. Consider
Perhaps more concretely, !!35\choose11!! is 417,225,900, which is small enough to fit in a 32-bit unsigned integer, but the algorithm I wrote wants to calculate this as !!35{34\choose10}\over11!!, and the numerator here is 4,589,484,900, which does not fit. One Reddit user suggested that you can get around this as follows: To multiply r by a/b, first check if b divides r. If so, calculate (r/b)·a; otherwise calculate (r·a)/b. This should avoid both overflow and fractions. Unfortunately, it does not. A simple example is !!{14\choose4} = {11\over1}{12\over2}{13\over3}{14\over4}!!. After the first three multiplications one has 286. One then wants to multiply by 14/4. 4 does not divide 286, so the suggestion calls for multiplying 286 by 14/4. But 14/4 is 3.5, a non-integer, and the goal was to use integer arithmetic throughout.
I haven't looked, but it is hard to imagine that Volume II of Knuth doesn't discuss this in exhaustive detail, including all the stuff I just said, plus a bunch of considerations that hadn't occurred to any of us.
A few people also pointed out that you can save time when n
> m/2 by calculating !!m\choose m-n!! instead of
[Other articles in category /math] permanent link |





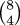 for example. The algorithm, as I wrote
it, calculates intermediate values 8, 8, 56, 28, 168, 56, 280, 70, and
70 is the final answer. If your computer has 7-bit machine integers,
the answer (70) will fit, but the calculation will overflow along the
way at the 168 and 280 steps.
for example. The algorithm, as I wrote
it, calculates intermediate values 8, 8, 56, 28, 168, 56, 280, 70, and
70 is the final answer. If your computer has 7-bit machine integers,
the answer (70) will fit, but the calculation will overflow along the
way at the 168 and 280 steps. . For example, instead of calculating !!100\choose98!!, calculate
. For example, instead of calculating !!100\choose98!!, calculate 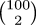 . I didn't mention this in the original article
because it was irrelevant to the main point, and because I thought it
was obvious.
. I didn't mention this in the original article
because it was irrelevant to the main point, and because I thought it
was obvious.