CARVIEW

MOTORHOMES

Select Language

HTTP/2 200 server: nginx date: Tue, 30 Dec 2025 06:07:01 GMT content-type: text/html; charset=UTF-8 vary: Accept-Encoding x-hacker: Want root? Visit join.a8c.com/hacker and mention this header. host-header: WordPress.com vary: accept, content-type, cookie link: ; rel=shortlink content-encoding: gzip x-ac: 4.bom _dca MISS alt-svc: h3=":443"; ma=86400 strict-transport-security: max-age=31536000 server-timing: a8c-cdn, dc;desc=bom, cache;desc=MISS;dur=543.0 Hard Arithmetic

Lang’s theorem — Pt. IV: a mixed-characteristic variant

This is a continuation of this post, this post, and this post. In it we formulate the correct mixed characteristic version of Lang’s theorem and give a proof using ideas from $p$ -adic Hodge theory. In doing so, we give an alternative understanding of Lang’s theorem giving rise to a reformulation that works far beyond the finite field case.

(more…)

Lang’s theorem — Pt. III a torsor reinterpretation and manifold applications

This is a continuation of this post and this post. Namely, use our discussion of torsors from the previous post to give a reinterpretation of Lang’s theorem. This will allow us to more concretely explain a multitude (but still just a small slice) of interesting implications of Lang’s theorem, and thereby understand how significant this result is for the study of finite fields.

(more…)

Lang’s theorem — Pt II: an interlude on torsors

This is a continuation of this post. Here we will discuss the various ways one can view torsors in anticipation of applying this to deduce some interesting corollaries of Lang’s theorem.

(more…)

Lang’s theorem — Pt. I: the classical result

In this post we discuss Lang’s theorem (i.e., that the Lang isogeny $x\mapsto x\sigma(x)^{-1}$ on $G(\overline{\mathbb{F}}_q)$ is surjective, for $G/\mathbb{F}_q$ a connected group variety) and an integral analogue of this result. This will allow us to discuss a lot of interesting arithmetic geometry, including the usefulness for the multitude of ways to interpret torsors.

(more…)

Shimura varieties and their integral canonical models (Pt. 2)

This is a continuation of this post.

§3 How and why?

Before we continue, I think it’s worth pausing to ask the above two questions about Shimura varieties.

§3.1 How?

While the moduli description in Expectation (exp:Shim-var) might provide a workable theory (at least in a theoretical sense), it’s entirely non-evident how people work with Shimura varieties given the harsh, arithmetically opaque, nature of their construction. So, how do people work with them?

Of course, there are a multitude of answers to this question. But, let me list a few very general ideas for how people work with Shimura varieties in practice.

Archimedean-type methods

Shimura varieties, by their very design are objects of an Archimedean (Hodge theory) provenance. It’s perhaps not shocking that some of the most powerful methods to actually proving this about Shimura varieties exploit fundamentally Archimedean theories. For example, the following ideas are routinely used to understand general Shimura varieties:

Archimedean Hodge theory,
differential-geometric and geometric-group-theoretic ideas (e.g., Margulis superridigity),
methods of logic applied to the analytic world (i.e., $O$ -minimality).

Special points

As indicated by Step 4 of the construction of Shimura varieties, the only truly tractable approach to them in an (obviously) arithmetically useful way is to use special points, where we do completely understand the arithmetic. This applies beyond the construction, and reducing to special points is one of the most common ways to prove something about general Shimura varieties.

“Type theory”

As will be discussed below, Shimura varieties can be ‘filtered by complexity’ into certain ‘types’. For low-complexity Shimura varieties (although they are not so simple!) one can really define an honest-to-god arithmetically-useful moduli problem in the vision of Expectation (exp:Shim-var). It is a common technique people apply to try and prove things about higher-complexity types by reducing them down the complexity ladder to these more approachable Shimura varieties.

Remark: I have explicitly left out a tantalizing direction here: $p$ -adic (Hodge-theoretic) methods. That is because this will essentially be the perspective taken in this series of lectures, and so I will delay their discussion until later. $\blacklozenge$

§3.2 Why?

Given all of this to-do about Shimura varieties, especially given the relative distance we are from making Expectation (exp:Shim-var) real, you have to wonder: is the juice is worth the squeeze?

Of course, at least for me, the answer is yes. Let me give three (of many possible more) reasons why I personally feel this is the case.

§3.2.1 Langlands

The canonical, and ‘correct’, answer is the Langlands program. In remarkably vague terms, Langlands posits a rough triangular correspondence between three of the most important pillars in modern mathematics:

I won’t attempt to try and define either $\mathbf{G}$ -valued Galois representations or automorphic representations of $\mathbf{G}$ –for more information on them (and what I am about to say below), see this post.

Remark: In fact, the more familiar reader will know that it’s not even $\mathbf{G}$ -valued Galois representations that appear here (even at a rough approximation). Namely, it should be $L$ -parameters for $\mathbf{G}$ –in particular it’s closer to ${^L}\mathbf{G}$ -valued Galois representations. That said, for the sake of space I will ignore this important point. $\blacklozenge$

But, Langlands gave something even finer than the above picture. He posited what sort of more primitive object actually is connecting the above three pillars: Shimura varieties. Namely, one should have something as indicated by the following diagram:

The vertical arrow should be obvious given Expectation (exp:Shim-var), but let me give a small idea of how Shimura varieties are related to Galois representations and automorphic representations and, in fact, connects them. (For more details see the above-linked post.)

Conjecture (Langlands–Kottwitz): There exists a decomposition

$\displaystyle H^\ast_\mathrm{\acute{e}t}(\mathrm{Sh}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)=\varinjlim_{\mathsf{K}}H^*_{\mathrm{\acute{e}t}}(\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)\simeq \bigoplus_{\pi}\rho_\pi\boxtimes \pi_f\qquad (\ast)$ ,

such that $\rho_\pi$ is $r_{-\mu_h}\circ \mathrm{GLC}(\pi)$ .

Let us tease out the meaning of the terms here:

Via the Hecke action, and the normal Galois action on étale cohomology, the left-hand carries an action of $\mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})\times\mathbf{G}(\mathbb{A}_f)$ .
The right-hand side is the decomposition of the left-hand side into irreducibles for the action of $\mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})\times\mathbf{G}(\mathbb{A}_f)$ , so $\rho_\pi$ is a representations of $\mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})$ and $\pi_f$ is a representation of $\mathbf{G}(\mathbb{A}_f)$ .
The index set $\pi$ travels over automorphic representations of $\mathbf{G}$ . These are, by definition, representations of $\mathbf{G}(\mathbb{A})$ and, as it turns out, always decompose into a box product $\pi_f\boxtimes \pi_\infty$ for the decomposition $\mathbf{G}(\mathbb{A})=\mathbf{G}(\mathbb{A}_f)\times\mathbf{G}(\mathbb{R})$ .
Finally, $r_{-\mu_h}$ is a certain representation of ${^L}\mathbf{G}$ , and $\mathrm{GLC}(\pi)$ is the global Langlands correspondence applied to $\pi$ .

In other words, the cohomology of Shimura variety realizes the global Langlands conjecture.

Other applications to algebraic geometry/number theory/harmonic analysis/differential geometry

While Langlands is maybe the marquee application of Shimura varieties, they have found nearly endless applications to other areas of algebraic geometry, number theory, and harmonic analysis.

Let me just give an example of an application for each of these fields which I find interesting:

Algebraic geometry: Madapusi used Shimura varieties to prove the Tate conjecture (a conjecture of fundamental importance in algebraic geometry) for K3 surfaces over finite fields (see [Madapusi]).
Number theory: The proof of the averaged Colmez conjecture by Andreatta–Goren–Howard–Madapusi (also proved independently by Yuan–Zhang), a conjecture relating heights on CM abelian varieties to special values of $L$ -functions, made use of orthogonal Shimura varieties (see [AGHM]).
Harmonic analysis: It was long a question of whether or not automorphic forms admit $p$ -adic interpolations. The answer (in many cases) is yes, and the definition involves Shimura varieties and their cohomology (e.g., see [Hida]).

A measuring stick for understanding of motives

Lastly, and most vaguely, but also close to my own heart, is the following. Over time we are getting closer and closer to trying to make Expectation (exp:Shim-var), and its correct ‘arithmetic generalizations’, a reality. For instance, the theme of this series of posts is that one can get an understanding of certain ‘canonical integral models’ of Shimura varieties using something tanatlizingly in the directions of a $p$ -adically integral analogue of Expectation (exp:Shim-var).

I find this ability of Shimura varieties as a metric for how far along our inexorable journey towards understanding ‘motives’ we are, to be one of the most beautiful aspects of the subject.

§4 “Type theory”

We mentioned above that there is a sort of “type theory” for Shimura varieties that naturally filters them by complexity. We would now like to explore this (to shallow depth), especially as the type of penultimate complexity, those of ‘abelian type’, factor heavily into future posts.

Modular curves

We start with the most basic (non-trivial), and classic class of Shimura varieties: modular curves.

Namely, let us fix:

$\mathbf{G}=\mathrm{GL}_2$ ,
$X=\mathfrak{h}_1^{\pm}=\mathbb{C}-\mathbb{R}$ which is the $\mathrm{GL}_2(\mathbb{R})$ -conjugacy class of the map

$h_0\colon \mathbb{C}^\times\to\mathrm{GL}_2(\mathbb{R}),\quad a+bi\mapsto \begin{pmatrix}a & -b\\ b & a\end{pmatrix}$ ,

$\mathsf{K}(N)=\ker\left(\mathrm{GL}_2(\widehat{\mathbb{Z}})\to\mathrm{GL}_2(\mathbb{Z}/N\mathbb{Z})\right)$ (assume $N\geqslant 3$ for simplicity).

Then, one may show that $(\mathrm{GL}_2,\mathfrak{h}^{\pm}_1)$ is a Shimura datum. And in fact, the associated Shimura varieties are the classical modular curves. Namely,

$\mathrm{Sh}_{\mathsf{K}(N)}(\mathrm{GL}_2,\mathfrak{h}_1^{\pm})\simeq Y(N):=\left\{(E,\alpha):\begin{aligned}(1)&\quad E\text{ is an elliptic curve},\\ (2)&\quad\alpha\colon (\mathbb{Z}/N)^2\simeq E[N].\end{aligned}\right\}^\simeq$

Siegel type

Modular curves are part of a general family of Shimura varieties, called Siegel type. In essence, they are the natural higher-dimensional generalizations of modular curves.

Namely, let us fix

$G=\mathrm{GSp}_{2g}$ –the symplectic similitude group, i.e., the group of linear automorphisms of $\mathbb{Q}^{2g}$ which preserves the standard symplectic form up to a scalar (the ‘similitude’),
$\mathfrak{h}^{\pm}_g$ is the so-called Siegel upper and lower half-spaces which can be shown to be the $\mathrm{GSp}_{2g}(\mathbb{R})$ -conjugacy class of a cocharacter,
$\mathsf{K}(N)=\ker\left(\mathrm{GSp}_{2g}(\widehat{\mathbb{Z}})\to\mathrm{GSp}_{2g}(\mathbb{Z}/N\mathbb{Z})\right)$ ( $N\geqslant 3$ ).

Then $(\mathrm{GSp}_{2g},\mathfrak{h}^{\pm}_g)$ is a Shimura datum, and the associated Shimura varieties are classifying the natural higher-dimensional analogues of what modular curves classify. Namely,

$\mathrm{Sh}_{\mathsf{K}(N)}(\mathrm{GSp}_{2g},\mathfrak{h}_g^{\pm}) \simeq \underbrace{\left\{(A,\lambda,\alpha):\begin{aligned}(1)&\quad A\text{ is an abelian variety},\\ (2)&\quad \lambda\text{ is a principal polarization of }A, \\ (3)&\quad\alpha\colon (\mathbb{Z}/N)^{2g}\simeq A[N]\text{ is a symplectic similitude}.\end{aligned}\right\}^\simeq}_{\mathscr{A}_{g,N}}$

In other words, Shimura varieties of Siegel type are the same as Mumford’s moduli space $\mathscr{A}_{g,N}$ of principally polarized abelian varieties together with $N$ level structure.

Remark: Let me roughly say what it means for $\alpha$ to be a symplectic similitude. Namely, $(\mathbb{Z}/N)^{2g}$ comes equipped with the standard symplectic pairing, and $A[N]$ obtains the symplectic pairing

$A[N]\times A[N]\xrightarrow{\lambda}A[N]\times A^\vee[N]\to \mu_N\simeq \mathbb{Z}/N.$

Because of this last isomorphism, this pairing is really only well-defined up to a scalar, but this doesn’t effect whether $\alpha$ is a symplectic similitude: i.e., whether it takes the standard pairing to this modified Weil pairing up to scalar. $\blacklozenge$

Remark: One may naturally expect the higher-dimensional analogues of modular curves should have group $\mathrm{GL}_g$ . But, there is no Shimura variety of the form $(\mathrm{GL}_g,X)$ when $g>2$ . This is easy enough to prove given the (unstated) conditions on $(\mathbf{G},X)$ , but perhaps less obvious is why is this the case from the algebro-geometric perspective.

Let me give two answers:

For $(\mathrm{GL}_g,X)$ , we would have $X = \mathrm{GL}_g(\mathbb{R})/\mathrm{O}(g)(\mathbb{R})$ which has (real) dimension $\tfrac{1}{2}g(g+1)$ . In particular, this is an odd-dimensional real manifold for unless $g=0,3\mod 4$ and so cannot be given a complex structure, and thus neither can the associated double quotient.
Secondly, the double quotient associated to $(\mathrm{GL}_g(\mathbb{C}),X)$ would be classifying (cf. the Siegel case) complex tori $\mathbb{C}^g/\Lambda$ . But, as observed in Remark (rem:Deligne-explained), such complex tori are generally not algebraizable, and thus neither can their moduli space. To fix this we need to add polarization as in loc. cit., but this then takes us to $\mathrm{GSp}_{2g}$ as in the Siegel case.
$\text{}$
(Take note of the following coincidence at play here: $\mathrm{GL}_2\simeq\mathrm{GSp}_2$ .)

In fact, it is perhaps reasonable to expect that with enough imagination one can construct ‘moduli spaces of global $\mathbf{G}$ -shtukas’ for any $\mathbf{G}$ , in analogy to the local picture, but which only exist as some sort of analytic stack in the flavor of Clausen–Scholze. Shimura varieties then should constitute, essentially, those such moduli spaces of shtukas which are algebraizable.

From this perspective, it’s shocking that Shimura varieties were discovered in the 60s and 70s: that long ago they identified an object whose ‘true context’ would not be definable for at least(!) 60 years. $\blacklozenge$

PEL, Hodge, Abelian, and General type

Beyond the Siegel case, Shimura varieties fall into ever increasingly more complicated ‘types’. It doesn’t quite make sense for me to spell out exactly what they mean rigorously here, and so instead let me just give a rough idea what they mean. Below, each class contains the previous one, and we give an example indicating a class not contained in any previous type.

PEL type

These classify principally Polarized abelian varieties $(A,\lambda,\alpha)$ with Level structure as in the Siegel case, but keep track of extra Endomorphism data in the form a ring map $\mathcal{O}\to\mathrm{End}(A)_{\mathbb{Q}}$ , for certain rings $\mathcal{O}$ . In particular, these do have moduli problems which work over any $S$ .

Example: The Shimura varieties of type $\mathrm{GU}(n-1,1)$ considered by Kottwitz, and used by Harris–Taylor to prove the local Langlands conjecture for $\mathrm{GL}_n$ , are of this type. $\blacklozenge$

Hodge type

These are those Shimura data $(\mathbf{G},X)$ which admit a closed embedding (called a Hodge embedding) into a Siegel datum $(\mathrm{GSp}_{2g},\mathfrak{h}^{\pm}_g)$ . From this embedding one is able to (non-canonically) define (via pullback) an abelian variety $A$ , and thus a motive, over $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)$ .

In the context of Expectation (exp:Shim-var), if $\omega^\mathrm{univ}$ is the ‘universal motive with $\mathbf{G}$ -structure’ over $\mathsf{Sh}_{\mathsf{K}}(\mathbf{G},X)$ , then $A$ is roughy $\omega(\mathbb{Q}^{2g})$ : the motive one gets by applying $\omega$ to the (chosen) Hodge embedding. But, we don’t know how to describe the motive $\omega(V)$ for other representations of $\mathbf{G}$ . In other words, we can non-conjecturally describe a motive on $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)$ , but we aren’t able to non-conjecturally put $\mathbf{G}$ -structure on it.

Example: Certain Shimura varieties $(\mathbf{G},X)$ , where $\mathbf{G}=\mathrm{GSpin}_g$ is the general spin group, are considered in [Madapusi] in the course of the proof for the Tate conjecture for K3 surfaces. $\blacklozenge$

Abelian type

I won’t try to give the rigorous definition of Shimura varieties of abelian type, but let me tell you the point. In the context of Expectation (exp:Shim-var), they are exactly those Shimura varieties whose associated motives with $\mathbf{G}$ -structure take values in the full subcategory $\mathbf{AbMot}(S)$ of abelian motives from §0.1.1.

Remark: As mentioned at the end of §0.1.2, abelian motives are objects that we can (at least conjecturally) define over smooth $\mathbb{C}$ -varieties $S$ , using the category $\mathbf{AbMot}^\mathrm{Hdg}(S)$ . In fact, using those, one can actually formulate and prove a version of Expectation (exp:Shim-var) as in [Milne7] and [Yang]. This is quite remarkable, and really lends some serious credence to Expectation (exp:Shim-var).

Unfortunately, for reasons mentioned at the end of §1, this is actually less useful than it first appears from an arithmetic perspective. One needs to beef up Expectation (exp:Shim-var) to handle, for example, $p$ -adic situations. That is why, in practice, even though Expectation (exp:Shim-var) does hold (at least up to blurring the lines between $\mathbf{AbMot}(S)$ and $\mathbf{AbMot}^\mathrm{Hdg}(S)$ ) it is rarely used. $\blacklozenge$

Example: This contains Shimura varieties of toral type, the famous Shimura curves (compact analogues of modular curves), and many more. In some sense, Shimura varieties of abelian type are perhaps the most ‘practically useful’ class of Shimura varieties (besides those of ‘preabelian type’), in the sense that they are large enough to contain most every example, but tractable enough to work with. $\blacklozenge$

General type

This is, in some sense, the wild west. Essentially nothing is known about such Shimura varieties from the perspective of Expectation (exp:Shim-var). In fact, in this case it’s not even clear (unlike the abelian case) how to single out what should be the smallest $\mathbb{Q}$ -linear $\otimes$ -subcategory of $\mathbf{VHS}_\mathbb{Q}(S)$ , for $S$ a quasi-comopact smooth $\mathbb{C}$ -variety, containing the motives that should show up in this context.

Example: Most famously, this contains the Shimura varieties with groups $E_6$ and $E_7$ . $\blacklozenge$

§5 Integral canonical models

In this final section we discuss one of the most interesting arithmetic aspects of Shimura varieties: the existence of ‘canonical integral models’ over various rings of integers.

Setup

To state things correctly, we first need to fix some extra notation:

let $v$ be a place $\mathbf{E}$ lying over $p$
set $E=\mathbf{E}_v$ (i.e., the completion of $\mathbf{E}$ at $v$ ), a finite extension of $\mathbb{Q}_p$ ,
let $\mathcal{O}_E$ be the ring of integers of $E$ , a finite extension of $\mathbb{Z}_p$ ,
and write $G=\mathbf{G}_{\mathbb{Q}_p}$ .

We then want to define a certain ‘integral canonical model’ of $\mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)_E$ over $\mathcal{O}_E$ . In fact, at least for now, I want this model to actually also be quasi-projective and smooth.

The smoothness condition for this model is quite serious and, in particular, shouldn’t happen for most levels $\mathsf{K}$ . Thus, we want to single out which sort of levels have a chance for giving us smooth models. This is encapsulated by the following definition.

Definition (defn:hyperspecial): A compact open subgroup $\mathsf{K}_0\subseteq G(\mathbb{Q}_p)$ is called hyperspecial if it is of the form $\mathcal{G}(\mathbb{Z}_p)$ for $\mathcal{G}$ a reductive model of $G$ over $\mathbb{Z}_p$ .

Remark: As it turns out, all reductive models $\mathcal{G}$ of $G$ over $\mathbb{Z}_p$ are abstractly isomorphic (see [Conrad, Theorem 7.2.16]). That said, this abstract isomorphism actually changes the associated hyperspecial subgroup $\mathcal{G}(\mathbb{Z}_p)\subseteq G(\mathbb{Q}_p)$ . Thus, while there is only one reductive group scheme model of $G$ , there are generally several non-conjugate classes of hyperspecial subgroups of $G(\mathbb{Q}_p)$ (e.g., see [Conrad, Example 7.2.15]). $\blacklozenge$

As per usual, write $\mathbb{A}_f=\mathbb{A}_f^p\times\mathbb{Q}_p$ . Then, we call a level of the form $\mathsf{K}=\mathsf{K}^p\mathsf{K}$ ,where $\mathsf{K}^p\subseteq \mathbf{G}(\mathbb{A}_f^p)$ and $K_0\subseteq G(\mathbb{Q}_p)$ is hyperspecial, hyperspecial at $p$ .

“Conjecture”(Langlands, Milne,…): If $\mathsf{K}$ is hyperspecial at $p$ , then there exists a “canonical” smooth quasi-projective $\mathcal{O}_E$ -model $\mathscr{S}_\mathsf{K}(\mathbf{G},X)$ of $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_E$ .

The reason that the word conjecture is in scare quotes is because of this wheedly word “canonical”. What does it mean? The most naive answer is “it should have the same moduli problem” (irrespective of Expectation (exp:Shim-var), I just mean this in a more naive sense). But, obviously this isn’t even approaching rigorous.

Let me give three possible better answers, none of which are maybe truly satisfying.

Answer 1: the Langlands–Rapoport conjecture

Recall from the Langlands–Kottwitz conjecture above, that the cohomology of Shimura varieties is meant to realize the global Langlands correspondence in some sense.

Of course, a natural question is: how does one even begin to approach proving such a statement? In fact, it’s helpful to instead step back and ask another even more fundamental question: how does one even understand any continuous Galois representations $\rho\colon \mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})\to \mathrm{GL}_n(\overline{\mathbb{Q}}_\ell)$ ? Namely, the source is a famously un-understandable group.

But, up to questions about semi-simplicitly (crucial/difficult ones we gloss over here!), there is a natural sort of numerical approach. Namely, by the Chebotarev density theorem the set

$\left\{\mathrm{Fr}^n_v\right\}_v\subseteq \mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})$ ,

consisting of choices of Frobenius lifts at all finite places $v$ of $\mathbf{E}$ is dense. Thus, it is enough to understand the set of numbers $\{\mathrm{tr}(\rho(\mathrm{Fr}^n_v))\}_v\subseteq \overline{\mathbb{Q}}_\ell$ by the Brauer–Nesbitt theorem.

OK, this seems nice. But, how do we understand these numbers. Well, let’s now assume that $\rho$ actually comes the étale cohomology groups $H^{i}_\mathrm{\acute{e}t}(S_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)$ for some (for simplicity) smooth proper $\mathbf{E}$ -scheme $S$ . Then, assuming $S$ has a smooth proper model $\mathcal{S}_v$ at $v$ , it follows from the famous smooth proper base change theorem that

$\displaystyle \mathrm{tr}\left(\mathrm{Fr}^n_v|H^i_\mathrm{\acute{e}t}(S_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)\right)=\mathrm{tr}\left(\mathrm{Fr}^n_q| H^i_\mathrm{\acute{e}t}(\mathcal{S}_{\overline{\mathbb{F}_p}},\overline{\mathbb{Q}}_\ell)\right)$

where $\mathrm{Fr}_q$ is the usual (geometric) $q$ -Frobenius map, where the residue field has size $q$ .

We make one last simplifying change: instead of an indvidual cohomology group $H^i$ , we take the alternating sum $\sum_i (-1)^i H^i$ . Thus, formally, we get

$\displaystyle \sum_i (-1)^i \mathrm{tr}\left(\mathrm{Fr}^n_v|H^i_\mathrm{\acute{e}t}(S_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)\right)=\sum_i (-1)^i \mathrm{tr}\left(\mathrm{Fr}^n_q| H^i_\mathrm{\acute{e}t}(\mathcal{S}_{\overline{\mathbb{F}_p}},\overline{\mathbb{Q}}_\ell)\right)$ .

But, this last term is something that has some concrete meaning! Namely, it’s the famous result of the Grothendieck–Lefschetz trace formula that this is just the cardinality $\#\mathcal{S}(\mathbb{F}_{q^n})$ which, at least ostensibly, is something one may be able to actually realistically compute!

So, how does this connect back the notion of ‘canonicalness’ of the model $\mathcal{S}_{\mathsf{K}}(\mathbf{G},X)$ ? Well, in short, Langlands (and later made precise by Langands–Rapoport, see [Milne8], which is why it is now called the Langlands–Rapoport conjecture) expect that such a model being ‘canonical’ should mean that there is a motivic description for each of the sets $\mathcal{S}_\mathsf{K}(\mathbf{G},X)(\mathbb{F}_{q^n})$ for all $n$ . And, more to the point, that this motivic description could lend itself to explicitly computing the size of this set. To what end? Well, that this point count is explicitly enough that, as part of the general discussion above, one could understand cohomology of Shimura varieties finely enough to prove the Langlands–Kottwitz conjecture.

Remark: There is a subtlety being elided here, but for which there is a brilliant trick to fix! What is the subtlety? It suffices to prove the Langlands–Kottwitz conjecture level-by-level, i.e., to show that for each level $\mathsf{K}$ there is an isomorphism

$\displaystyle H^\ast_\mathrm{\acute{e}t}(\mathrm{Sh}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)^\mathsf{K}=H^*_{\mathrm{\acute{e}t}}(\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)\simeq \bigoplus_{\pi}\rho_\pi\boxtimes \pi_f^\mathsf{K}$ ,

where, as per usual, $(-)^\mathsf{K}$ means fixed points. As the above indicates, one could try to prove this by performing point counting arguments at hyperspecial places of $\mathsf{K}$ . But, of coruse, $\mathsf{K}$ is not going to be hyperspecial for all places (i.e., the Shimura variety is not going to have good reduction at all places). So it’s not immediately evident that the above idea is enough.

But, the finer point of Chebotarev density saves the day. Not only are the powers of Frobenii at all places dense, but actually one can omit finitely many places and still maintain density. As $\mathsf{K}$ is hyperspecial at $p$ for almost all $p$ (i.e., the Shimura variety is good reduction at almost all places), this is actually enough! $\blacklozenge$

Answer 2: motivic expectation

Given Expectation (exp:Shim-var), it is tantalizing to imagine that one could qualify ‘canonicalness’ by giving a motivic description of the $S$ -points of $\mathscr{S}_\mathsf{K}(\mathbf{G},X)$ for a $\mathcal{O}_E$ -scheme $S$ . But, how do we make this preicse?

First, observe that as we want $\mathscr{S}_\mathsf{K}(\mathbf{G},X)$ to be flat and separated over $\mathcal{O}_E$ it suffices, by Yoneda, to restrict our attention to shemes $S$ flat and separated over $\mathcal{O}_E$ . Then $S_E$ is (schematically) dense in $S$ . Thus, the map

$\mathrm{Hom}(S,\mathscr{S}_{\mathsf{K}}(\mathbf{G},X))\to \mathrm{Hom}(S_E,\mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X))$

is injective. The upshot of this is that the data of a map $S\to \mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)$ is actually a property about the associated map $S_E\to\mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)$ . Let us call this property good reduction. Thus, we see that giving a motivic understanding of $\mathscr{S}_{\mathsf{K}}(\mathbf{G},X)$ boils down to giving a motivic criterion for the map $S_E\to\mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)$ to be of good reduction.

But, how do we give such a good reduction criterion? An answer may not be immediately forthcoming, but a good hint is given by our setup: we should consider the reductive model $\mathcal{G}/\mathbb{Z}_p$ of $G=\mathbf{G}_{\mathbb{Q}_p}$ . Namely, let us say that $\mathbb{Q}_p$ -motive $\nu$ with $G$ -structure over $S_E$ has good reduction if it has an integral model, i.e., there exists a $\mathbb{Z}_p$ -motive with $\mathcal{G}$ -structure $\nu^\circ$ on $S$ such that $\nu=\nu^\circ[\tfrac{1}{p}]|_{S_{\mathbb{Q}_p}}$ .

A tantalizing conjecture may then be the following. To state it, let $\omega^\mathrm{univ}$ be the hypothetical universal $\mathbb{Q}$ -motive with $\mathbf{G}$ -structure on $\mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)$ , and let $\omega^\mathrm{univ}\otimes\mathbb{Q}_p$ be the associated $\mathbb{Q}_p$ -motive with $G$ -structure.

Meta-conjecture:A morphism $f\colon S_E\to \mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)$ has good reduction if and only if the $\mathbb{Q}_p$ -motive with $G$ -structure $f^\ast(\omega^\mathrm{univ}\otimes\mathbb{Q}_p)$ has good reduction.

Of course, as of now, we are very far from making this precise: we don’t know how to define a $\mathbb{Q}$ -motive for a smooth $\mathbb{C}$ -scheme, so the prospect of defininig a $\mathbb{Z}_p$ -motive on a $\mathcal{O}_E$ -scheme seems entirely out of reach…or is it? We will discuss this more in subsequent posts.

Answer 3: an extension property

While historically there has not been a precise definition of what it means for a single model $\mathscr{S}_\mathsf{K}(\mathbf{G},X)$ to be canonical, there has been a precise definition for what an entire system $\{\mathscr{S}_{\mathsf{K}_0\mathsf{K}^p}(\mathbf{G},X)\}_{\mathsf{K}^p}$ (i.e., as the level away from $p$ varies) of models $\{\mathrm{Sh}_{\mathsf{K}_0\mathsf{K}^p}(\mathbf{G},X)\}_{\mathsf{K}^p}$ .

Here by a ‘model’ of the system, I mean not only that we have models for each indvidual level, but we have models for the Hecke action. We say that this action is by finite étale morphisms if each $[g]_{-}$ and $\pi_{-,-}$ are finite étale morphisms (even integrally).

Definition (Langlands, Milne,…): A system of smooth $\mathcal{O}_E$ -models $\{\mathscr{S}_{\mathsf{K}_0\mathsf{K}^p}(\mathbf{G},X)\}$ is integral canonical if the Hecke action is by finite étale morphisms, and the following extension property holds: for every formally smooth $\mathcal{O}_E$ -algebra $R$ , the natural map

$\displaystyle \varprojlim_{\mathsf{K}^p}\mathscr{S}_{\mathsf{K}_0\mathsf{K}^p}(\mathbf{G},X)(R)\to \varprojlim_{\mathsf{K}^p}\mathrm{Sh}_{\mathsf{K}_0\mathsf{K}^p}(\mathbf{G},X)(R[\tfrac{1}{p}])$ ,

is a bijection.

It’s a little bit hard to understand what this extension property, something like a Néron model property at infinite level, has anything to do with being a ‘canonical integral model’. In essence, one should think of it as encoding a sort of Néron–Ogg–Shafarevich property, as indicated by the following Siegel-type example.

Example (eg:ICM-Siegel): Let us fix $N\geqslant 3$ and a prime $p$ . Then, the level

$\mathsf{K}(N)\subseteq\mathrm{GSp}_{2g}(\mathbb{A}_f)$

is hyperspecial at $p$ if and only if $p\nmid N$ . In this case, the integral canonical model of the system $\{\mathscr{A}_{g,N}\}_{p\nmid N}$ is…the same thing. What I mean is that the exact same moduli problems for each such $\mathscr{A}_{g,N}$ represents a smooth quasi-projective system over $\mathbb{Z}_p$ , and that together they form an integral canonical models. The only non-obvious point here is the following: why does the extension property hold? The anser: the Néron–Ogg–Shafarevich theorem (see [FaltingsChai, Theorem 6.7]).

Namely, suppose that we have a sequence of points $(A,\lambda,\alpha_N)$ in $\varprojlim \mathscr{A}_{g,N}(R[\tfrac{1}{p}])$ . Then, we have compatible isomorphisms $\alpha_N\colon (\mathbb{Z}/N)^{2g}\xrightarrow{\sim}A[N]$ for all $N$ . Passing to the limit we see, for example, that for any prime $\ell\ne p$ we have an isomorphism $T_\ell(A)\simeq \mathbb{Z}_\ell^{2g}$ –an isomorphism of étale sheaves. In particular, being trivial means certainly that $T_\ell(A)$ is unramified (in the appropriate suitable sense), and what the Néron–Ogg–Shafarevich theorem tells us is that this implies that $A$ has good reduction, i.e., it admits an abelian variety model $\mathcal{A}$ over $R$ . It’s simple to check that both $\lambda$ and $\alpha_N$ (for all $N$ ) naturally lift to $\mathscr{A}$ , and so the sought after point of $\varprojlim \mathscr{A}_{g,N}(R)$ is $(\mathcal{A},\lambda,\alpha_N)$ . $\blacklozenge$

This example helps clarify the relationship betwen the extension property and the Meta-conjecture. Namely, through the lens of the Meta-conjecture the extension property says something simple: at infinite level the pullback of the motive $\omega^\mathrm{univ}\otimes\mathbb{Q}_p$ always has good reduction. Indeed, in the Siegel-type case this is exactly the relevant consequence of the Néron–Ogg–Shafarevich criterion.

So, to underscore the point, one can think of the extension property as a distillation of this fact: it says something weaker than the Meta-conjecture–it doesn’t tell us which maps $f$ have the property that $f^\ast(\omega^\mathrm{univ}\otimes\mathbb{Q}_p)$ has good reduction at finite level, but declares that this always happens at infinite level.

Remark (rem:role-of-hyperspecial): A natural question is what role did the hyperspecialness play in the above discussion? Saying it rigorously is mildly difficult without a large diversion, but you can get the idea just by looking at the last step of Example (eg:ICM-Siegel). Namely, we said that the level structures $\alpha_N\colon (\mathbb{Z}/N)^{2g}\to A[N]$ naturally lift to level structures $\alpha_N\colon (\mathbb{Z}/N)^{2g}\to \mathcal{A}[N]$ . The fact that this was possible was due to the fact that $p\nmid N$ . In fact, if $p\mid N$ , then this moduli problem makes no sense: its special fiber would be empty as $A[p]$ is never isomorphic to $(\mathbb{Z}/p)^{2g}$ .

In general, $p$ -adic étale theory does not work well when $p$ is not invertible, and so any hope of having the ‘same moduli problem’ as one might hope for integral canonical models (e.g., as happened in Example (eg:ICM-Siegel)) will require that nothing can be happening at $p$ with the leve lstructure. And, as hinted at in Remark (rem:lvl-str), one should think that hyperspecial-at- $p$ level structure indeed corresponds to the ‘partial trivialization’ imposing no conditions at $p$ . $\blacklozenge$

Known cases

Now, while the idea of integral canonical models is highly interesting, and potentially highly profitable, it seems almost impossible to imagine how to rigorously approach their construction. Indeed, as we have emphasized in this post, Shimura varieties, and particularly their arithmetic, are quite opaque. As we have now mentioned several times, even Expectation (exp:Shim-var) is not enough to save us as it cannot really deal with varieties over $E$ , let alone over $\mathcal{O}_E$ .

Given this, it’s perhaps surprising to know that integral canonical models (in the system sense) have been constructed in a huge swath of cases.

Theorem: An integral canonical model $\{\mathscr{S}_{\mathsf{K}_0\mathsf{K}^p}(\mathbf{G},X)\}_{\mathsf{K}^p}$ of $\{\mathsf{Sh}_{\mathsf{K}_0\mathsf{K}^p}(\mathbf{G},X)\}_{\mathsf{K}^p}$ exists when $(\mathbf{G},X)$ is of:

Siegel type ([FaltingsChai], 1990),

abelian type ([Kisin], 2009),

general type when $p\gg 0$ ([BST], 2024).

Remark: There is also the relevant work of Vasiu (e.g., as in [Vasiu]). See [Moonen, §5] for a discussion of this work and interesting ideas it contains. $\blacklozenge$

So, in essence, the only remaining cases of Langlands integral canonical models conjecture (at least in the system of models sense) are the caes of general type Shimura varieties for small $p$ .

OK, so given the daunting nature of constructing arithmetic models of arithmetically-opaque, Shimura varieties, how were the above results proven? The answer, in incredibly broad terms, is as follows (with corresponding numbering):

classical (the models themselves are quite old even if the Néron–Ogg–Shafarevich theorem in the generality needed here is more recent),
type theory (this is done by a sophisticated devissage to the Siegel type case) and some non-trivial integral $p$ -adic Hodge theory (used to show smoothness of the construction),
very powerful algebraic geometry/ $p$ -adic Hodge theory techniques which applies in a much more general setup, and for which applications to integral canonical models are (in some sense) an afterthough.

So, two basic questions which remain in the conjecture of integral canonical models are:

Question 1: How can one characterize integral canonical models at individual level (opposed to the fully system), and in a more motivic fashion, i.e., rigorously realize the above Meta-conjecture?

Question 2: How can one construct integral canonical models for general type Shimura varieties at small primes (preferably with some addtional motivic structure)?

The goal of this series of lectures is to, essentially try to give one answer to Question 1.

§6 A toy example

In this last section I just want to give an idea for what an answer to the above-stated Question 1 might look like in the simplest of all cases: the case of modular curves.

To this end, I want to state a very contrived-sounding question which serves as a warmup to Question 1. The explicit relationship to Question 1 will be follwed up on in subsequent posts.

Question 1′: Can one characterize the integral canonical model of modular curves using only ‘at $p$ data’?

Statement of the theorem

Let me tease out the meaning of Question 1′ a bit more. For simplicitly, let us write $Y(N)$ instead of $Y(N)_{\mathbb{Q}_p}$ . Then, as indicated in Example (eg:ICM-Siegel), the integral canonical model of the modular curve $Y(N)$ (where $N\geqslant 3$ and $p\nmid N$ ) over $\mathbb{Z}_p$ is…the same modular curve.

Namely, it is

$\mathcal{Y}(N):=\left\{(\mathcal{E},\alpha):\begin{aligned}(1)&\quad \mathcal{E}\text{ is an elliptic curve},\\ (2)&\quad \alpha\colon (\mathbb{Z}/N)^2\simeq\mathcal{E}[N].\end{aligned}\right\}$

In other words, $\mathcal{Y}(N)$ has the identical moduli problem to $Y(N)$ except the elliptic curve $E$ in the former is only allowed to live over a $\mathbb{Q}_p$ scheme, whereas the elliptic curve $\mathcal{E}$ in the latter is allowed to live over any $\mathbb{Z}_p$ -scheme (thus the change in notation).

Given this, the answer to Question 1′, at least at first blush, is obivously no. Very clearly the moduli problem for $\mathcal{Y}(N)$ needs the full elliptic curve $\mathcal{E}$ and this doesn’t just contain ‘at $p$ -information’, e.g., it contains the information of the $\ell$ -adic Tate module $T_\ell(\mathcal{E})$ for any prime $\ell\ne p$ . But, a close inspection shows that the Meta-conjecture does posit something exactly like this: our criterion for good reduction didn’t involve the $\mathbb{Q}$ -motive with $\mathbf{G}$ -structure, but only its base change to $\mathbb{Q}_p$ . So, let’s forge ahead undeterred.

To give a better sense of what ‘at $p$ information’ means here, let me list two objects associated to $\mathcal{Y}(N)$ .

The $p$ -adic Tate module:

Let $f\colon E^\mathrm{univ}\to Y(N)$ be the universal family of elliptic curves over $Y(N)$ . Set

$T_p(E^\mathrm{univ}):=(R^1 f_\ast \underline{\mathbb{Z}}_p)^\vee$ ,

a rank two $\mathbb{Z}_p$ -local system.

It is useful to note that from the perspective of Expectation (exp:Shim-var), $V_p(E^\mathrm{univ}):=T_p(E^\mathrm{univ})[\tfrac{1}{p}]$ is nothing more than the $p$ -adic realization of the universal motive $\mathbb{Q}$ -motive with $\mathrm{GL}_2$ -structure (i.e., $E^\mathrm{univ}$ )

The $p$ -divisible group

Let $\mathcal{E}^\mathrm{univ}$ be the universal family of elliptic curves over $\mathcal{Y}(N)$ and let $\mathcal{E}^\mathrm{univ}[p^\infty]$ be its associated $p$ -divisible group. From the perspective the Meta-conjecture, one should view this as the $\mathbb{Z}_p$ -motive $\mathrm{GL}_{2,\mathbb{Z}_p}$ which ‘models’ $E^\mathrm{univ}\otimes\mathbb{Q}_p$ .

Remark: For reaspons of space I won’t try to justify this last claim here, as it will be the focus of future posts. But, in essence, one should think of $p$ -divisible groups as being something like $1$ -motives with $\mathbb{Z}_p$ -coefficients, i.e., that they’re like the ‘at $p$ version of abelian varieties’. Thus, the object $\mathcal{E}^\mathrm{univ}[p^\infty]$ really is motivic in nature. $\blacklozenge$

We are now ready to state our answer to Question 1′, using only the above two pieces of at $p$ data. To state the result it will be convenient to give ourselves a little more notation:

$\widehat{\mathcal{Y}}(N)$ denote $p$ -adic completion of $\mathcal{Y}(N)$ , thought of as $p$ -adic formal scheme,
$\mathrm{BT}_p$ as the moduli space of $p$ -divisible groups
$\rho\colon \widehat{\mathcal{Y}}(N)\to\mathrm{BT}_p$ the map determined by $\mathcal{E}^\mathrm{univ}[p^\infty]$ (explicitly, it associates to a point $(\mathcal{E},\alpha)$ of $\mathcal{Y}(N)$ the $p$ -divisible group $\mathcal{E}[p^\infty]$ ).

Theorem (toy example):The following two properties of $\mathcal{Y}(N)$ hold, and uniquely characterize it as a separated model of $Y(N)_{\mathbb{Q}_p}$ :

Serre–Tate: the morphism $\rho\colon\widehat{\mathcal{Y}}(N)\to\mathrm{BT}_p$ is formally étale,

Crystalline locus: a (classical) point $x$ of the rigid analytic space $Y(N)_{\mathbb{Q}_p}^\mathrm{an}$ lies in the open subset $\widehat{\mathcal{Y}}(N)_\eta$ if and if $T_p(E^\mathrm{univ})_x$ is crystalline.

There’s a lot to unpack here, and it will require us to to finish the next two posts to fully flesh things out. But, for a bare-bones understanding, let me just say the following two things:

The ‘formal étaleness’ in the Serre–Tate statement is the usual one algebraic geometers are familiar with. But, roughly, just means that the map $\rho$ establishes an identification between the deformation theory of $\widehat{\mathcal{Y}}(N)$ and $\mathrm{BT}_p$ .
$\text{}$
The crystalline locus statement involved the phrase “ $T_p(E^\mathrm{univ})_x$ is crystalline”. Here one can think of the ‘classical point’ $x$ as just an $F$ -point $(E_x,\alpha_x)$ of $Y(N)$ for a finite extension $F/E$ . Then, the $\mathbb{Z}_p$ -local system pulled back to $x$ can be thought of a as the $p$ -adic Galois representation of $F$ given by $T_p(E_x)$ .
$\text{}$
It is then a classical notion in $p$ -adic Hodge theory for such a representation to be crystalline which, in broad terms, one should think of as saying that the local system has ‘good reduction’. We will discuss this idea more in depth in future posts.

What is a scheme over 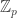$\mathbb{Z}_p$ anyways?

Perhaps the most in-your-face part of Theorem (toy example) which is not intially expected is the amount of formal and rigid geometry. We don’t have time to really discuss either of these topics seriously. For that I wholeheartedly recommend the survey [FujiwaraKato] (or this less useful previous post).

Instead, I just want to take a moment to explain why formal and rigid geometry ought to show up here. After all, we were after a model of the scheme $Y(N)$ over $\mathbb{Z}_p$ –who decided to introduce $p$ -adic analytic things into the mix? My contention is, in fact, that it is impossible to avoid it.

To help understand this claim, let me ask the reader to picture a scheme over $\mathbb{Z}_p$ . Perhaps the most common picture for such a thing is the following:

You have a base space $\mathrm{Spec}(\mathbb{Z}_p)$ with two points, $\mathrm{Spec}(\mathbb{Q}_p)$ and $\mathrm{Spec}(\mathbb{F}_p)$ , and your fibers over those two points.

I claim that a much more accurate picture of the situation is, instead, the following (taken from [AchingerYoucis]):

The specifics of the symbols here don’t matter, and neither does the base really. Instead focus on the melting flan on top. The

base of this melting flan is a scheme $U$ over $\mathbb{Q}_p$ ,
the body of the flan constitutes a formal scheme $\mathfrak{X}$ over $\mathbb{Z}_p$ ,
the scheme in its totality is then the result of gluing $\mathfrak{X}$ to $U$ along the open region in $U$ labeled $\mathfrak{X}^\mathrm{rig}$ or, maybe more commonly written, $\mathfrak{X}_\eta$ –the Raynaud generic fiber of $\mathfrak{X}$ .

But, just to nail the point home, this open region we are gluing along is rigid analytic, i.e., it only exists as an open subset of the analytic space $U^\mathrm{an}$ associated to $U$ .

The upshot of this is the following: a $\mathbb{Z}_p$ -scheme $\mathscr{X}$ may be thought of as the result of gluing the formal scheme $\widehat{\mathscr{X}}$ to the $\mathbb{Q}_p$ -scheme $\mathscr{X}_{\mathbb{Q}_p}$ along the common rigid analytic (i.e., adic space) open subset $\mathscr{X}_{\mathbb{Q}_p}^\mathrm{an}\supseteq \widehat{\mathscr{X}}_\eta\subseteq \widehat{\mathscr{X}}$ , which we may call the anchor set of the gluing.

One may equationally express this idea as follows:

$\mathscr{X}=\mathscr{X}_{\mathbb{Q}_p}\sqcup_{\widehat{\mathscr{X}}_\eta}\widehat{\mathscr{X}}$

This is not pure fantasy either, as can be made precise by the main theorem of [AchingerYoucis] which says that one can, in fact, (up to enlarging to algebraic spaces) perform the reverse: any formal $\mathbb{Z}_p$ -scheme $\mathfrak{X}$ glued to a $\mathbb{Q}_p$ -scheme $U$ along rigid analytic open embedding $\mathfrak{X}_\eta\hookrightarrow U^\mathrm{an}$ is an algebraic object!

The triple $(U,\mathfrak{X},j\colon \mathfrak{X}_\eta\hookrightarrow U^\mathrm{an})$ is what we call a gluing triple. So, in words, the main theorem of [AchingerYoucis] says that (up to subtleties related to algebraic spaces) schemes over $\mathbb{Z}_p$ are the same as gluing triples.

Example (eg:gluing-triple-A1): One can physically see the rigid geometry at work even in the simplest example: $\mathscr{X}=\mathbb{A}^1_{\mathbb{Z}_p}$ . Indeed, what is the connection between $\mathbb{A}^1_{\mathbb{Z}_p}$ and its generic fiber $\mathbb{A}^1_{\mathbb{Q}_p}$ ? Well, perhaps the most obvious one is $\mathbb{A}^1_{\mathbb{Z}_p}(\mathbb{Z}_p)\subseteq\mathbb{A}^1_{\mathbb{Q}_p}(\mathbb{Q}_p)$ . But, I hope the reader won’t mind me being cute and pointing out

$\mathbb{A}^1_{\mathbb{Z}_p}(\mathbb{Z}_p)=\mathbb{Z}_p=\{x\in\mathbb{Q}_p:|x|\leqslant 1\}\subseteq\mathbb{Q}_p=\mathbb{A}^1_{\mathbb{Q}_p}$ .

A rigid analytic open subset has appeared, and it’s not a coincidence or trick. $\blacksquare$

From the gluing triple perspective, the rigid and formal geometry appearing in Theorem (toy example), comes into focus. Characterizing $\mathcal{Y}(N)$ as a model of $Y(N)$ only requires two pieces of information as one part of the gluing triple $Y(N)=\mathcal{Y}(N)_{\mathbb{Q}_p}$ is fixed as part of the setup. Those two pieces of data are

the rigid analytic open anchor set in $Y(N)^\mathrm{an}$ we want to glue along (which ultimately is $\widehat{\mathcal{Y}}(N)_\eta$ ),
a way to characterize the formal scheme (which is ultimately $\widehat{\mathcal{Y}}(N)$ ) we will glue to $Y(N)$ along this anchor set.

From this perspective the crystalline locus part of Theorem (toy example) is exactly addressing the first of these peices of information (i.e., pinning down the anchor set), and the Serre–Tate theorem is (perhaps non-obvious) addressing the second (by characterizing the formal scheme we will glue to the anchor set).

In fact, we also see the inevitability of rigid geometry even in the Meta-conjecture. Namely, the natural generalization of Example (eg:gluing-triple-A1) fact always holds: if $\mathscr{X}$ is a scheme over $\mathbb{Z}_p$ , then the subset

$\mathscr{X}(\mathbb{Z}_p)\subseteq \mathscr{X}(\mathbb{Q}_p)=\mathscr{X}_{\mathbb{Q}_p}^\mathrm{an}(\mathbb{Q}_p)$

is always rigid analytic and, moreover, an analagous statement holds with $\mathbb{Z}_p$ replaced by any scheme over it. But, from this perspective, Meta-conjecture naturally will involve rigid geometry as this image set is (by construction) the good reduction locus: so the good reduction locus is always a rigid analytic object.

In some sense, this is what the crystalline locus part of Theorem (toy example) was telling us, but it perhaps is a little hard to internalize if you aren’t familiar with the notion of crystalline. So, instead, let me give a much more visually clear illustration of the fact that the good reduction locus in $Y(N)$ is a rigid-analytic object.

Recall that there is a $j$ -invariant map $j\colon Y(N)\to\mathbb{A}^1_{\mathbb{Q}_p}$ . There is then a famous result that an elliptic curve has (potentially) good reduction if and only if it’s $j$ -invariant has norm at most one. In symbols this says

$\left\{\begin{matrix}\text{Good reduction}\\\text{locus in }Y(N)\end{matrix}\right\}=\widehat{\mathcal{Y}}(N)_\eta=j^{-1}(\{|x|\leqslant 1\})$ ,

a patently rigid-analytic open subset.

References

[AchingerYoucis] https://arxiv.org/pdf/2410.20500

[AGHM] Andreatta, F., Goren, E., Howard, B. and Madapusi Pera, K., 2018. Faltings heights of abelian varieties with complex multiplication. Annals of Mathematics, 187(2), pp.391-531.

[BST] https://arxiv.org/pdf/2405.12392

[Baez] https://arxiv.org/pdf/2304.08737

[Broshi] Broshi, M., 2013. G-torsors over a Dedekind scheme. Journal of Pure and Applied Algebra, 217(1), pp.11-19.

[Conrad] https://math.stanford.edu/~conrad/papers/luminysga3.pdf

[CMSP] Carlson, J., Müller-Stach, S. and Peters, C., 2017. Period mappings and period domains. Cambridge University Press.

[Deligne1] https://www.numdam.org/item/SB_1970-1971__13__123_0.pdf

[Deligne2] https://publications.ias.edu/sites/default/files/34_VarietesdeShimura.pdf

[Deligne3] https://www.numdam.org/item/PMIHES_1971__40__5_0.pdf

[FujiwaraKato] Fujiwara, K. and Kato, F., 2006. Rigid geometry and applications. Moduli spaces and arithmetic geometry, Adv. Stud. Pure Math, 45, pp.327-386.

[GenestierNgo] https://www.math.uchicago.edu/~ngo/Shimura.pdf

[Hida] Hida, H., 2004. p-adic automorphic forms on Shimura varieties. New York: Springer.

[Hoermann] https://fhoermann.org/shimura2.pdf

[Kerr] https://www.math.wustl.edu/~matkerr/SV.pdf

[Kisin] Kisin, M., 2010. Integral models for Shimura varieties of abelian type. Journal of the American Mathematical Society, 23(4), pp

[Kottwitz1] Kottwitz, R.E., 1984. Shimura varieties and twisted orbital integrals. Mathematische Annalen, 269(3), pp.287-300.

[Lan] https://www.kwlan.org/articles/intro-sh-ex.pdf

[Madapusi] Madapusi Pera, K., 2015. The Tate conjecture for K3 surfaces in odd characteristic. Inventiones mathematicae, 201(2), pp.625-668.

[Milne1] https://www.jmilne.org/math/xnotes/svi.pdf

[Milne2] https://www.jmilne.org/math/articles/1994bP.pdf

[Milne3] https://www.jmilne.org/math/xnotes/MOT.pdf

[Milne4] https://www.jmilne.org/math/articles/DT.pdf

[Milne5] Milne, J.S., 1983. The action of an automorphism of C on a Shimura variety and its special points. In Arithmetic and Geometry: Papers Dedicated to IR Shafarevich on the Occasion of His Sixtieth Birthday Volume I Arithmetic (pp. 239-265). Boston, MA: Birkhäuser Boston.

[Milne6] https://www.jmilne.org/math/articles/1990aT.pdf

[Milne7] https://www.jmilne.org/math/xnotes/svh.pdf

[Milne8] https://www.jmilne.org/math/xnotes/Montreal.pdf

[Moonen] https://www.math.ru.nl/~bmoonen/Papers/SMCfinal.pdf

[Morel] https://fhoermann.org/shimura2.pdf

[Rosen] Rosen, M., 1986. Abelian varieties over C. Arithmetic geometry, pp.79-101.

[Serre] https://www.numdam.org/item/SCC_1958-1959__4__A10_0.pdf

[Vasiu] Vasiu, A., 1999. Integral canonical models of Shimura varieties of preabelian type. Asian Journal of Mathematics, 3, pp.401-517.

[Yang] https://arxiv.org/pdf/2304.10751

Shimura varieties and their canonical integral models (Pt. 1)

This will (hopefully) be the first in a series of four posts based off a lecture series given at the Morningside Center of Mathematics in Beijing. The goal overall is to talk about some recent advances in the $p$ -adic geometry of Shimura varieties and their integral canonical models. The goal of this (essentially standalone) post more specifically is to give a sort of broad overview for what Shimura varieties and their integral canonical models are, and why one should care about them.

It is a fool’s errand to try and define Shimura varieties in any sort of rigorous way in such a small amount of time, and I will make zero attempt to do so here. For that I can only point to other references, some of which I list here: [Deligne1], [Deligne2], [GenestierNgo], [Hida], [Hoermann], [Kerr], [Lan], [Milne1], [Milne2], [Moonen], [Morel].

Disclaimer: For the sake of exposition, the below will take many non-trivial liberties, most of which are about ideas for which it’s difficult to even make rigorous sense of. For this reason, I caution the reader for taking anything written here too seriously, and to treat it only as vague motivation. I apologize in advance to any experts who take issue with these inaccuracies.

§0 motives and objects with $H$ -structure

Below we will frequently make use of the ideas of ‘motives’ and objects with ‘ $H$ -structure’. We take a sort of primitivist approach to these notions, not trying too seriously to even describe the desiderata they are meant to satisfy. That said, to help orient the unfamiliar reader, let me say a few words below on each.

§0.1 Motives

(I cannot possibly do justice to the idea of motives here, especially in addressing the subtleties for what such a fantastic theory would entail. For that I can only suggest consulting the much more enlightening references [Milne3] and [Baez] (and especially the references discussed in §5 of the latter).)

For the uninitiated, one can think of the category of $\mathbf{Mot}_R(S)$ of $R$ -motives on $S$ (for a ring $R$ and scheme $S$ ) as being the receptacle for an ‘optimal’ cohomology theory

$H^\ast_\mathrm{mot}\colon \mathbf{SmProj}(S)\to\mathbf{Mot}_R(S)$ ,

on the category $\mathbf{SmProj}(S)$ of smooth projective $S$ -schemes. Namely, we expect that $\mathbf{Mot}_R(S)$ should be something like an $R$ -linear $\otimes$ -category. Roughly this means you can $R$ -linearly add morphisms in $\mathbf{Mot}_R(S)$ , take tensor products in $\mathbf{Mot}_R(S)$ (in a way that is $R$ -linear although I won’t demand the tensor product is ‘over $R$ ‘), and that you can make sense of exact sequences in $\mathbf{Mot}_R(S)$ .

The ‘optimality’ here means that for any other ‘reasonable’ cohomology theory $H_\mathcal{C}\colon \mathbf{SmProj}(S)\to \mathcal{C}$ , where $\mathcal{C}$ is (for simplciitly) an exact $R$ -linear $\otimes$ -category, there should be a factorization

where ${R}_\mathcal{C}\colon \mathbf{Mot}_R(S)\to \mathcal{C}$ is some ‘realization functor’. So, any extra structure that the category $\mathcal{C}$ could contain (Galois action, filtration, Hodge structure,…) should somehow already be captured in $\mathcal{C}$ , thus making $\mathbf{Mot}_R(S)$ the ‘richest category of cohomological invariants’.

Again, we are taking a very primitivist perspective here, mostly out of necessity. Motives in any naive sense like I am trying to describe them ‘less than exist’: forgetting their existence, there isn’t even a guess of what the category is (or what properties it should satisfy), especially over the type of general bases $S$ that I have allowed here. I just want to mention two cases at which one can gesture towards motivic thinking in the way I mean it here.

Remark: For the sake of some readers’ sanity, let me point out that there do exist precisely defined notions of ‘motives’, e.g., Voevodsky motives. The relationship to the idealized vaugery of motives we mean here is largely conjectural, especially over general bases $S$ . So, somehow the ‘rigorously defined’ motives considered in, for example, motivic cohomology, don’t directly facet into our discussion. $\blacklozenge$

§0.1.1 Abelian varieties

The category $\mathbf{Mot}_R(S)$ should carry something like a ‘weight grading’ which, in rough terms, should be related to the degree of cohomology, i.e., which $H^i_\mathrm{mot}$ , we are taking. For $1$ -motives with coefficients in $\mathbb{Q}$ (i.e., $R=\mathbb{Q}$ ) there is a very rough idea for what the category of $1$ -motives should be: abelian schemes.

Namely, there should something like a fully faithful embedding

$\mathbf{AbVar}(S)_{\mathbb{Q}}\to\mathbf{Mot}_\mathbb{Q}(S)$

where the source is the isogeny category of abelian varieties (i.e., the localization of $\mathbf{AbVar}(S)$ along the class of isogenies. The map

$H^1_\mathrm{mot}\colon \mathbf{SmProj}(S)\to \mathbf{AbVar}(S)$

should very roughly send $X$ to its Albanese variety.

This idea stands up to some amount of scrutiny via the fact that first cohomology groups of most cohomology theories depend only on the associated Albanese variety:

$H^1_\mathcal{C}(X)=H^1_\mathcal{C}(\mathrm{Alb}(X))$ .

In other words, one roughly has $H^1_\mathcal{C}=H^1_\mathcal{C}\circ H^1_\mathrm{mot}$ , in line with the ‘optimality’ we would want $H^1_\mathrm{mot}$ to satisfy.

Remark: On the other hand, some readers may also see how abjectly absurd the above is in its oversimplicity. The Albanese variety does not exist for arbitrary bases (although it does exist over reduced varieties over an algebraically closed field as in [Serre]). Moreover, when it exists, the Albanese variety is usually not an abelian scheme itself, but a torsor for an abelian scheme. So, at best, one may believe that (isogeny classes of) abelian varieties do fully faithfully embed into the category of $1$ -motives with $\mathbb{Q}$ -coefficients. But even more dire is that the fact that $H^1_\mathcal{C}$ factorizes through the Albanese does not always hold for all bases $S$ and all cohomology theories. Again this discussion of motives is meant more for flavor and not so much for precision. $\blacklozenge$

Now, one cannot perform linear algebra operations in $\mathbf{AbVar}_\mathbb{Q}(S)$ like tensor product, i.e., it’s not an exact $\mathbb{Q}$ -linear $\otimes$ -category, and this property will be quite important when discussing $H$ -objects below. But, as $\mathbf{Mot}_\mathbb{Q}(S)$ does enjoy these properties, one can form the smallest exact $\mathbb{Q}$ -linear $\otimes$ -subcategory of $\mathbf{Mot}_\mathbb{Q}(S)$ containing $\mathbf{AbVar}(S)$ . This is called the category of abelian motives over $S$ , and is denoted $\mathbf{AbMot}(S)$ .

§0.1.2 Archimedean Hodge theory

It is a classic observation that comes for Archimedean Hodge theory, that one has a functor

$\displaystyle H^\ast_\mathrm{Betti}\colon \mathbf{SmProj}(\mathbb{C})\to \mathbf{Hdg}_\mathbb{Q},\quad X\mapsto H^\ast_\mathrm{sing}(X(\mathbb{C}),\mathbb{Q})\otimes_{\mathbb{Q}}\mathbb{C}\simeq \bigoplus_{p+q=\ast}H^q(X,\Omega^p)$ ,

where $\mathbf{Hdg}_\mathbb{Q}$ is the category of (pure) $\mathbb{Q}$ -Hodge structures. In other words, the singular cohomology $H^\ast_\mathrm{sing}(X(\mathbb{C},\mathbb{Q})$ of the underlying projective complex manifold $X(\mathbb{C})$ , together with the Hodge decomposition of $H^\ast_\mathrm{sing}(X(\mathbb{C}),\mathbb{Q})\otimes_{\mathbb{Q}}\mathbb{C}\simeq H^\ast_\mathrm{sing}(X(\mathbb{C}),\mathbb{C})$ , allows one to build from $X$ a $\mathbb{Q}$ -Hodge structure. Now, the theory of motives would dictate that there should be a realization functor

$R_\mathrm{Hdg}\colon \mathbf{Mot}_\mathbb{Q}(\mathbb{C})\to \mathbf{Hdg}_\mathbb{Q}$

such that $R_{\mathrm{Hdg}}(H^\ast_\mathrm{mot}(X))=H^\ast_\mathrm{Betti}(X)$ . Moreover, one can essentially interpret the Hodge conjecture as saying that $R_\mathrm{Hdg}$ is fully faithful.

This extends to the relative situation, where for a smooth $\mathbb{C}$ -variety $S$ one can define the category $\mathbf{VHS}_\mathbb{Q}(S)$ of variations of $\mathbb{Q}$ -Hodge structures, which are like a holomorphically varying family of objects $V_s\in\mathbf{Hdg}_\mathbb{Q}$ for $s\in S(\mathbb{C})$ . One then has a functor

$H^\ast_\mathrm{Betti}\colon \mathbf{SmProj}(S)\to \mathbf{VHS}_\mathbb{Q}(S),\quad H^\ast_\mathrm{Betti}(X):=R^\ast f^\mathrm{an}_\ast\underline{\mathbb{Q}}$ ,

where $f^\mathrm{an}\colon X(\mathbb{C})\to S(\mathbb{C})$ is the induced morphism of complex manifolds. One also expects from the Hodge conjecture that the realization functor $R_\mathrm{Hdg}\colon \mathbf{Mot}_\mathbb{Q}(S)\to \mathbf{VHS}_\mathbb{Q}(S)$ in this relative setting is fully faithful.

Let me emphasize the upshot here. The Hodge conjecture predicts that the category of $\mathbb{Q}$ -motives over a quasi-compact smooth $\mathbb{C}$ -variety are a full subcategory of (variations of) $\mathbb{Q}$ -Hodge structures. This means that, at least conjecturally, all possible cohomological information that could be contained in a smooth projective $S$ -scheme is already contained in its Betti cohomology. Thus, in some sense this shifts our attention from constructing the category of motives in some abstract sense, and instead to singling out the ‘correct’ subcategory of Hodge structures. In particular, this gives a sort of ‘cheating’ way to get at motives: we can instead work with Archimedean Hodge theory as a substitute…at least for smooth $\mathbb{C}$ -varieties.

To see how this connects with abelian varieties, we recall the following result of Deligne.

Proposition [Deligne3, Rappel (4.4.3)]: Let $S$ be a quasi-compact smooth variety over $\mathbb{C}$ . Then, there is an equivalence of categories

$H^1_\mathrm{Betti}\colon \mathbf{AbVar}(S)\to \mathbf{PolVHS}^{\{(-1,0),(0,-1)\}}_\mathbb{Z}(S)$ .

Here the target category is the category of variations of $\mathbb{Z}$ -Hodge structures which are

polarizable,
of type $\{(-1,0),(0,-1)\}$ –this just means that these are the only pairs of $(p,q)$ that show up in the Hodge decomposition.

Remark (rem:Deligne-explained): This theorem can be made a lot less daunting in the case $S=\mathrm{Spec}(\mathbb{C})$ , and it further helps explain this polarizability condition. Namely, one can check that if $\Lambda$ is a finite free $\mathbb{Z}$ -module, then a $\mathbb{Z}$ -Hodge structure of type $\{(-1,0),(0,-1)\}$ on it amounts to a complex structure on $\Lambda\otimes_\mathbb{Z}\mathbb{R}$ , in particular the rank of $\Lambda$ is even, say $2g$ . One may then consider the quotient $(\Lambda\otimes_\mathbb{Z}\mathbb{R})/\Lambda$ which is an abelian variety of dimension $g$ …or is it!

In the case of dimension $1$ (i.e., $g=1$ ) this truly is the case as all such lattice quotients are elliptic curves. But, for $g>1$ these are, in general, non-algebraizable complex tori. The exact condition needed to guarantee that they algebraizable is that this complex torus possesses a Riemann form (see [Rosen, §3]) which amounts to the claim that the associated Hodge structure is polarizable. $\blacklozenge$

In particular, Deligne’s theorem tells us that $H^1_\mathrm{Betti}$ gives us a fully faithful embedding of $\mathbf{AbVar}(S)$ into $\mathbf{VHS}_\mathbb{Q}(S)$ . Then, we can apply this ‘cheating’ mindset here. Above we defined the full subcategory $\mathbf{AbMot}(S)_\mathbb{Q}\subseteq\mathbf{Mot}_\mathbb{Q}(S)$ of abelian motives, i.e., the $\mathbb{Q}$ -linear $\otimes$ -category generated by abelian varieties in $\mathbf{Mot}_\mathbb{Q}(S)$ . By the Hodge conjecture this should be identified with its image in $R_\mathrm{Hdg}$ and agree with the $\mathbb{Q}$ -linear $\otimes$ -category generated by $\mathbf{AbVar}(S)_\mathbb{Q}$ in $\mathbf{VHS}_\mathbb{Q}(S)$ . But, we can actually rigorously define this last category!

To underscore this, if we take $\mathbf{AbMot}^\mathrm{Hdg}(S)$ , for a smooth $\mathbb{C}$ -variety $S$ , to be the full $\mathbb{Q}$ -linear $\otimes$ category generated by $\mathbf{AbVar}(S)_\mathbb{Q}$ in $\mathbf{VHS}_\mathbb{Q}(S)$ , this is a non-conjectural way of defining what ought to be equivalent to category $\mathbf{AbMot}(S)$ of (true) abelian motives over $S$ . But, of course, the category $\mathbf{AbMot}^\mathrm{Hdg}(S)$ , unlike $\mathbf{AbMot}(S)$ , is non-conjectural!

§0.2 Objects with $H$ -structure

Recall as above that for a ring $R$ an exact $R$ -linear $\otimes$ -category is one where you can $R$ -linearly add morphisms, take tensor products, and that you can make sense of exact sequences.

The key example of this is as follows.

Example: Let $H$ be a (finite type, affine, smooth) group scheme over $R$ . Then, the category $\mathbf{Rep}_R(H)$ of (finite $R$ -projective) representations of $H$ is an $R$ -linear exact $\otimes$ -category in the obvious way. $\blacklozenge$

Definition (defn:H-objects): The category $H\text{-}\mathscr{C}$ of $H$ -objects in $\mathscr{C}$ is the category of exact (i.e., sends exact sequences to exact sequences) $R$ -linear $\otimes$ -functors

$\omega:\mathrm{Rep}_R(H)\to \mathscr{C}$ .

Perhaps the most illuminating example of this idea is the following.

Example (e.g., see [Broshi]): Let $X$ be a scheme over a DVR $R$ . Then, the category $\mathbf{Vect}(X)$ of vector bundles on $X$ is an exact $R$ -linear $\otimes$ -category in the obvious way, and $H\text{-}\mathbf{Vect}(X)$ identifies with the category $\mathbf{Tors}_H(X)$ of $H$ -torsors on $X$ . $\blacklozenge$

In particular, I would implore the reader to think of $H$ -objects in $\mathscr{C}$ (at least up to first approximation) as being something like ‘ $H$ -torsors in $\mathscr{C}$ ‘.

§1 A dreamland: moduli of motives

We begin by trying to describe Shimura varieties $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)$ as they ought to be. As is indicated by the notation, such varieties are built using the input of the data $(\mathbf{G},X)$ and $\mathsf{K}$ . The first of these, the more important of the two, is the following.

Definition (defn:shim-data): A Shimura datum is a pair $(\mathbf{G},X)$ consisting of

$\mathbf{G}$ a reductive group over $\mathbb{Q}$ ,

$X=\{h_x\}_{x\in X}\in \mathrm{Hom}(\mathbb{S},\mathbf{G}_\mathbb{R})/\mathbf{G}(\mathbb{R})\text{-conj.}$ ,

such that … . Its Hodge cocharacter $\mu_h=\{\mu_x\}\in\mathrm{Hom}(\mathbb{G}_{m,\mathbb{C}},\mathbf{G}_\mathbb{C})/\mathbf{G}(\mathbb{C})\text{-conj.}$ is defined by $\mu_x(z)=h_x(z,1)$ for any $h_x$ .

A morphism of Shimura data $f\colon (\mathbf{G}_1,X_1)\to (\mathbf{G}_2,X_2)$ is a morphism $f\colon\mathbf{G}_1\to \mathbf{G}_2$ of $\mathbb{Q}$ -groups such that $f(X_1)\subseteq X_2$ , and is a closed embedding if $\mathbf{G}_1\to\mathbf{G}_2$ is.

Let me make some comments on some of the structures appearing in this definition:

The group $\mathbb{S}=\mathrm{Res}_{\mathbb{C}/\mathbb{C}}(\mathbb{G}_{m,\mathbb{C}})$ (i.e., $\mathbb{C}^\times$ viewed as a real algebraic group) is the so-called Deligne torus. It is the Tannakian fundamental group of the Tannakian category $\mathbf{Hdg}_\mathbb{R}$ of real Hodge structures (with the usual fiber functor).
$\text{}$
So, $\mathrm{Hom}(\mathbb{S},\mathbf{G}_\mathbb{R})/\mathbf{G}(\mathbb{R})\text{-conj.}$ is naturally identified with $(\mathbf{G}\text{-}\mathbf{Hdg}_\mathbb{R})^{\simeq}$ (the notation $\simeq$ means ‘isomorphism classes’). In particular, one may view the $X$ in a Shimura datum as being an isomorphism class of real Hodge structures equipped with $\mathbf{G}$ -structure.
$\text{}$
One has a natural (up to normalization) identification $\mathbb{S}_\mathbb{C}=\mathbb{G}_{m,\mathbb{C}}\times\mathbb{G}_{m,\mathbb{C}}$ thus the notation on the right-hand side of $\mu_x(z)=h_x(z,1)$ makes sense.
$\text{}$
From the perspective that $X$ is an isomorphism class of objects in $\mathbf{G}\text{-}\mathbf{Hdg}_\mathbb{R}$ , one may $\mu_h$ view as the (conjugacy class of) cocharacter(s) defining the Hodge filtration on these real Hodge structures, whence the name.

We are actually already almost at the naive definition of $\mathrm{Sh}_K(\mathbf{G},X)$ , and only need one extra piece of notation/terminology.

Definition(defn:reflex-field): The reflex field $\mathbf{E}=\mathbf{E}(\mathbf{G},X)$ of the Shimura datum $(\mathbf{G},X)$ is the field of definition of $\mu_h$ .

Remark: There is a small subtlety about the phrase ‘field of definition’ for a conjugacy class of cocharacters. Namely, it is possible that the action of $\mathrm{Aut}(\mathbb{C})$ on such conjugacy classes fixes $\mu_h$ as a conjugacy class, but fixes no actual element in $\mu_h$ . In other words, there needn’t actually be a cocharacter in $\mu_h$ defined over $\mathbf{E}$ . That said, this subtlety disappears (see [Kottwitz1, Lemma 1.1.3]) with the mild assumption that $\mathbf{G}$ is quasi-split (i.e., has a rationally-defined Borel). $\blacklozenge$

So, we are already ready to try and ‘define’ what $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)$ is. Namely, it is meant to be a smooth quasi-projective $\mathbf{E}$ -variety, and thus (by Yoneda) to characterize it, it is enough to tell you the value $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(S)$ for a smooth quasi-compact $\mathbf{E}$ -variety $S$ .

Expectation (exp:Shim-var): For a smooth quasi-compact $\mathbf{E}$ -variety $S$ ,

$\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(S)=\left\{\begin{matrix}\mathbb{Q}\text{-motives with }\mathbf{G}\text{-structure }\omega\text{ of type}\\ X\text{ and with }\mathrm{\acute{e}}\text{tale }\mathsf{K}\text{-level structure}\end{matrix}\right\}^{\simeq}$

To try and explain what the meaning of these extra terms ‘type $X$ ‘ and ‘étale $\mathsf{K}$ -level’ structure means, let us set up some notation. Namely, a $\mathbb{Q}$ -motive on $S$ with $\mathbf{G}$ -structure is an exact $\mathbb{Q}$ -linear $\otimes$ -functor $\omega\colon \mathbf{Rep}_\mathbb{Q}(\mathbf{G})\to \mathbf{Mot}_\mathbb{Q}(S)$ . We then obtain a diagram as follows

Here

$R_\ell\colon \mathbf{Mot}_\mathbb{Q}(S)\to\mathbf{Loc}_{\mathbb{Q}_\ell}(S)$ is the $\ell$ -adic étale realization functor, so the output is an étale $\mathbb{Q}_\ell$ -local system,
$R_\mathrm{Hdg}\colon \mathbf{Mot}_\mathbb{Q}(S)\to\mathbf{VHS}_\mathbb{Q}(S)$ is the Hodge realization functor, so the output is a variation of $\mathbb{Q}$ -Hodge structure .

We are then defining $\omega_\ell$ and $\omega_\mathrm{Hdg}$ to make the diagram commute (i.e., they are $\ell$ -adic and Hodge realization of $\omega$ , respectively).

We can then describe the above-mentioned conditions on $\omega$ as follows:

Type $X$ : This means that for every $\mathbb{C}$ -point $s$ of $S$ one has that $(\omega_\mathrm{Hdg})_s\otimes\mathbb{R}\simeq X$ , i.e., that the pullback to $s$ of the Hodge realization of $\omega$ is isomorphic to $X$ in $(\mathbf{G}\text{-}\mathbf{Hdg}_\mathbb{R})^\simeq$ , i.e., we’re fixing the pointwise isomorphism class of our real Hodge structures to be $X$ .

Note that as $S$ is defined over $\mathbf{E}$ , there is an action of $\mathrm{Aut}(\mathbb{C}/\mathbf{E})$ on $S(\mathbb{C})$ , and so the above condition should be stable under such an action. But, as $\mathbf{E}$ is defined (roughly) to be the (smallest) field where the isomorphism class of $X$ makes sense, this tracks.

Étale $\mathsf{K}$ -level structure: Here we are fixing a compact open subgroup $\mathsf{K}\subseteq\mathbf{G}(\mathbb{A}_f)$ (where $\mathbb{A}_f=\widehat{\mathbb{Z}}\otimes_\mathbb{Z}\mathbb{Q}$ ). Then such a level structure is a global section of the sheaf

$\underline{\mathrm{Isom}}((\omega_\ell),(\omega_\ell^\mathrm{triv}))/\mathsf{K}$ .

Remark (rem:lvl-str): Let us tease this out slightly more. Here $\omega_\ell^\mathrm{triv}$ is the trivial $\mathbb{Q}_\ell$ -local system with $\mathbf{G}$ -structure: it associates to a representations $V$ of $\mathbf{G}$ the constant local system $V\otimes_{\mathbb{Q}}\underline{\mathbb{Q}}_\ell$ . One may then think of $\underline{\mathrm{Isom}}((\omega_\ell),(\omega_\ell^\mathrm{triv}))$ as the sheaf of ‘simultaneous trivalizations’ of the $(\omega_\ell)$ as $\ell$ varies. This naturally has an action of $\mathbf{G}(\mathbb{A}_f)$ as the automorphisms of $(\omega_\ell^\mathrm{triv})$ as a collection of $\mathbb{Q}_\ell$ -local systems with $\mathbf{G}$ -structure is $\mathbf{G}(\mathbb{A}_f)$ . Thus, we can take the quotient sheaf $\underline{\mathrm{Isom}}((\omega_\ell),(\omega_\ell^\mathrm{triv}))/\mathsf{K}$ , and an étale $\mathsf{K}$ -level structure is a global section of this.

This may be a bit hard to grok on first read, but the idea is roughly the following. As each $\omega_\ell$ is a $\mathbb{Q}_\ell$ -local system one can trivialize it (with $\mathbf{G}$ -structure) if one works ‘very locally’, e.g., over some masive pro-étale local cover $S'\to S$ . Now one does not expect any particular (family of) trivialization(s) $\omega_\ell\xrightarrow{\sim}\omega_\ell^\mathrm{triv}$ over $S'$ to descend to $S$ (i.e., you don’t expect $\omega_\ell$ to be trivial over $S$ ). But, descending a $\mathsf{K}$ -orbit of such trivializations has such a chance because this means that no particular trivialization on the nose descends, but it does up to ‘blurring’ (i.e., up to changing it by the action of $\mathsf{K}$ ).

The result of this, roughly, is that this allows only a ‘partial trivialization’ of $(\omega_\ell)$ . For example, as $\mathsf{K}\subseteq\mathbf{G}(\mathbb{A}_f)$ is compact open you know (roughly) that it corresponds to a product of compact open subgroups of $K_\ell\subseteq \mathbf{G}(\mathbb{Q}_\ell)$ as $\ell$ varies, and for almost all $\ell$ it must be something like $\mathcal{G}(\mathbb{Z}_\ell)$ for almost all $\ell$ . At these ‘hyperspecial’ places (more on this later) one can convince themselves that this partial trivialization says nothing: there is no condition on $\omega_\ell$ . For other ‘non-hyperspecial’ $\ell$ , a typical example of such a $K_\ell$ is $\ker(\mathcal{G}(\mathbb{Z}_\ell)\to \mathcal{G}(\mathbb{Z}/\ell^n\mathbb{Z}))$ , in which case one can roughly think that the ‘partial trivialization’ at $\ell$ is not a full trivialization of $\omega_\ell$ but a trivialization of $\omega_\ell\mod\ell^n$ (i.e., the reduction modulo $\ell^n$ of some $\mathbb{Z}_\ell$ -lattice in $\omega_\ell$ ). This is not a perfectly rigorous explanation, but it should hopefully give a sense for what’s going on. $\blacklozenge$

Expectation (exp:Shim-var) should immediately indicate to you why Shimura varieties are so important in arithmetic geometry: they are moduli spaces for motives, the object of centralmost importance in the linear algebra study of varieties. That said, this expectation is just that, an expectation:

As mentioned in §0, we don’t have any rigorous definition of $\mathbf{Mot}_\mathbb{Q}(S)$ , and so we’re foiled at the very first step of trying to make our expectation even a rigorous conjecture. But, there is some hope as $S/\mathbf{E}$ gives rise to a smooth $\mathbb{C}$ -variety $S_\mathbb{C}$ , one might apply Archimedean Hodge theory to approach things, as indicated in §0.1.2, especially in special (abelian type!) cases.
The hope of using Archimedean Hodge theory to put Expectation (exp:Shim-var) on more firm footing (as mentioned in 1.) is nice, but, in fact, the expectation itself is not nearly good enough to actually work with Shimura varieties as arithmetic-geometric objects. Namely, it doesnt’t cover the case when $S$ is smooth over a $p$ -adic field, which would be pivotal for studying (the base change of) Shimura varieties over fields like $\mathbb{Q}_p$ , a cornerstone of our modern approach to arithmetic geometry.
$\text{}$
In this $p$ -adic realm Archimedan Hodge theory can do nothing to help us. But, there is still some hope to work $p$ -adically: if Archimedean Hodge theory can’t work in the $p$ -adic world what about… $p$ -adic Hodge theory? More on this later.

Remark (conditions-on-(G,X)): In our ‘definition’ of Shimura datum, I never actually stated the conditions on $(\mathbf{G},X)$ they are required to satisfy. The reason for this is that they are opaque. But, let me vaguely say their purpose, and take this up again in the next section.

Namely, there is no a priori reason to believe that the functor described in Expectation (exp:Shim-var) should be representable by a scheme, i.e., that it should be algebraic. For example, our definition involves Archimedean Hodge theory, which is an inherently analytic theory–maybe this space should only exist analytically (in an appropriate sense)? Roughly these extra unstated conditions on $(\mathbf{G},X)$ are to guarantee that this algebraicity holds. $\blacklozenge$

§2 Harsh reality: the lifecycle of a Shimura variety

The dreamland from the last section must now collide with the grim meat-hook reality of Shimura varieties. Namely, while Expectation (exp:Shim-var) is beautiful it is, as we said, not workable in our current understanding of things. That said, Shimura varieties themselves aren’t conjectural: they are flesh-and-blood mathematical objects. So, what do they actually look like?

Remark: The more astute reader will notice that I am not making any assumptions on $\mathsf{K}$ below. Technically one needs to assume that $\mathsf{K}$ is a so-called neat subgroup to really get an algebraic variety. This is a technical point though that I will ignore. It also seems well-known among experts that this is somewhat of an illusory problem, and could be remedied by working with stacks in the appropriate categories at all stages. A similar issue (and solution) holds for the distinction between $\mathbf{G}$ and $\mathbf{G}^c$ , for those that know what that means. $\blacklozenge$

The construction, in steps

Let me describe, in the roughest of possible terms, the creation of Shimura varieties in four steps.

Step 1: real manifold

Shimura varieties start out life as something quite far from a smooth quasi-projective algebraic variety over the number field $\mathbf{E}$ : they start out as real manifolds.

Before we state this precisely, let us observe that as $X$ is a $\mathbf{G}(\mathbb{R})$ -conjugacy class we may write it as $X=\mathbf{G}(\mathbb{R})/\mathsf{K}_\infty$ for some subgroup $\mathsf{K}_\infty\subseteq\mathbf{G}(\mathbb{R})$ . In fact, the (unstated) conditions on $(\mathbf{G},X)$ force $\mathsf{K}_\infty$ to be the unique (up to conjugacy) maximal compact subgroup of $\mathbf{G}(\mathbb{R})$ . Regardless, it’s evident that $X$ inherits the structure of a real manifold from $\mathbf{G}(\mathbb{R})$ .

We then set

$\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C}):=\mathbf{G}(\mathbb{Q})\backslash X\times \mathbf{G}(\mathbb{A}_f)/\mathsf{K}=\mathbf{G}(\mathbb{Q})\backslash \mathbf{G}(\mathbb{A})/\mathsf{K}\mathsf{K}_\infty.$

Here $\mathbb{A}=\mathbb{A}_f\times\mathbb{R}$ , and $\mathbf{G}(\mathbb{Q})$ is acting diagonally on the product in the first expression whereas $\mathsf{K}$ is acting only on the $\mathbf{G}(\mathbb{A}_f)$ factor of the second expression.

Remark: As indicated by the notation $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ , this is the $\mathbb{C}$ -points of the eventual $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)$ . In particular, this looks miles away from Expectation (exp:Shim-var), but is slightly closer than these first appearances.

Namely, if $M$ is a $\mathbb{Q}$ -motive with $\mathbf{G}$ -structure as in Expectation (exp:Shim-var) (written $\omega$ there) then you could imagine considering the pair

$(M_\mathbb{R},(M_\ell)):=(R_\mathrm{Hdg}(M)\otimes\mathbb{R},(R_\ell(M))$ .

As we’re over $\mathrm{Spec}(\mathbb{C})$ , the étale $\mathsf{K}$ -level condition is literally just an element $(g_\ell)\mathsf{K}$ of the set

$\mathrm{Isom}((M_\ell),(M_\ell^\mathrm{triv}))/\mathsf{K}\simeq \mathbf{G}(\mathbb{A}_f)/\mathsf{K}$ .

Moreover, $M_\mathbb{R}$ determines an object of $\mathbf{G}\text{-}\mathbf{Hdg}_\mathbb{R}$ we know that it must belong to, by the Type $X$ condition, the isomorphism class $X$ . So, it corresponds to an element $x$ of $X$ .

As we are interested in isomorphism classes of such $M$ , the pair $(x,(g_\ell))\in X\times\mathbf{G}(\mathbb{A}_f)/\mathsf{K}$ . is in fact only well-defined up to isomorphism of $\mathbb{Q}$ -motives with $\mathbf{G}$ -structure, i.e., up to the of by $\mathbf{G}(\mathbb{Q})$ . Thus, we see that we only get a well-defined class in

$\mathbf{G}(\mathbb{Q})\backslash X\times \mathbf{G}(\mathbb{A}_f)/\mathsf{K}=\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ .

The sort of faith-based part of this then is that the theory of motives should imply that this association does actually form a bijection between this double-quotient set and the set of isomorphism classes appearing in Expectation (exp:Shim-var). $\blacklozenge$

Step 2: complex manifold

All connected components of $X$ are isomorphic, and so we fix one $X^+$ . One may then write

$\displaystyle \mathrm{Sh}_\mathsf{K}(\mathbf{G},X)\simeq \bigsqcup_i X^+/\Gamma_i$ ,

where the index set is finite and each $\Gamma_i\subseteq \mathbf{G}(\mathbb{Q})$ is an ‘arithmetic group’ (i.e., the intersection of a compact open subgroup of $\mathbf{G}(\mathbb{A}_f)$ with $\mathbf{G}(\mathbb{Q}$ ). Up to the finiteness of this index, this is just a simple exercise in writing this double quotient as a union of single quotients.

Thus, to put a complex manifold structure on $\mathsf{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ is tantamount to putting a complex manifold structure on the real manifold $X$ . And, this we can specify (and prove) using the (unstated) conditions on $(\mathbf{G},X)$ in a pleasing way.

Proposition (prop:cmplx-str): There exists a unique complex manifold structure on $X$ such that $\{h_x\}_x$ is an object of $\mathbf{VHS}_\mathbb{R}(X)$ , i.e., a variation of real Hodge structures.

In other words, we have sort of tailor made $X$ to be a period domain (i.e., a moduli space of Hodge structures, see [CMSP]).

Remark: Let me try to make this feel a little less abstract. Fix an element $\mu_0$ of the conjugacy class $\mu_h$ . This determines a unique parabolic $P_{\mu_0}\subseteq \mathbf{G}_\mathbb{C}$ (e.g., see [Conrad, Theorem 4.1.7]). The associated (partial) flag variety is the $\mathbb{C}$ -variety

$\mathcal{F}\ell_{\mu_0}:=\mathbf{G}_\mathbb{C}/P_{\mu_0}$ .

As $N_{\mathbf{G}_\mathbb{C}}(P_{\mu_0})=P_{\mu_0}$ , this space classifies the parabolics conjugate to $P_{\mu_0}$ . The isomorphism class of this partial flag variety doesn’t depend on the choice of $\mu_0$ , so we denote it by $\mathcal{F}\ell_{\mu_h}$ .

Observe then that we have a natural map of real manifolds

$X\to \mathcal{F}\ell_{\mu_h}(\mathbb{C})$ ,

sending $h_x$ to the conjugate parabolic $P_{\mu_x}$ . Then, ultimately, Proposition (prop:cmplx-str) amounts to the claim that there exists a unique complex manifold structure on $X$ such that the map $X\to\mathcal{F}\ell_{\mu_h}(\mathbb{C})$ is holomorphic (for any choice of $\mu_0$ ). $\blacklozenge$

Step 3: complex variety

Now comes what, to me, is perhaps the most miraculous part of the construction of Shimura varieties (although this is probably a function of my own mathematical weaknesses).

Theorem (Baily–Borel): There exists a unique smooth quasi-projective $\mathbb{C}$ -variety $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_\mathbb{C}$ with underlying complex manifold $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ such that for any other smooth quasi-projective $\mathbb{C}$ -variety the natural map

$\mathrm{Hom}\left(S,\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_\mathbb{C}\right)\to \mathrm{Hom}\left(S(\mathbb{C}),\mathrm{Sh}(\mathbf{G},X)(\mathbb{C})\right)$

is a bijection.

In words this says that there is a unique way to algebraize (to a smooth quasi-projective $\mathbb{C}$ -variety) $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})_\mathbb{C}$ such that any holomorphic map $S(\mathbb{C})\to \mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ , for a smooth quasi-projective $\mathbb{C}$ -variety $S$ , uniquely algebraizes.

One could perhaps view this through the lens of Expectation (exp:Shim-vars) as saying that the (unstated) conditions on $(\mathbf{G},X)$ force the type of motivic objects being classified to automatically be algebraizable, e.g., compare this to Deligne’s theorem from §0.1.2.

Remark: Let me try to make this ever so slightly less abstract. For a representation $V$ of $\mathbf{G}_\mathbb{C}$ one can build a holomorphic vector bundle $\mathbb{V}$ on the complex manifold $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ :

$\mathbb{V}:=\mathbf{G}(\mathbb{Q})\backslash X\times V\times\mathbf{G}(\mathbb{A}_f)/\mathsf{K}\to \mathbf{G}(\mathbb{Q})\backslash X\times\mathbf{G}(\mathbb{A}_f)/\mathsf{K}=\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ ,

where $\mathbf{G}(\mathbb{Q})$ is acting diagionally on $X\times V\times\mathbf{G}(\mathbb{A}_f)$ , where it’s action on $V$ is through the inclusion $\mathbf{G}(\mathbb{Q})\subseteq \mathbf{G}(\mathbb{C})$ , and $\mathsf{K}$ still only acts on $\mathbf{G}(\mathbb{A}_f)$ .

(Such a vector bundle is called an automorphic vector bundle. They in fact, as $V$ varies, define an object of $G_\mathbb{C}\text{-}\mathbf{Vect}(\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C}))$ , i.e., a $G$ -torsor on $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ .)

Take $V_\lambda$ for $\lambda$ a $\mu_h$ -dominant weight such that $\langle \lambda,\mu_h\rangle>0$ . One can show that

$\displaystyle \mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_\mathbb{C}^\ast:=\mathrm{Proj}\left(\bigoplus_{k\geqslant 0}H^0\left(\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C}),\mathbb{V}_\lambda^{\otimes k}\right)\right)$

defines a normal, connected, projective $\mathbb{C}$ -variety (although almost never smooth!), called the Baily–Borel compactification of the Shimura variety. Moreover, it’s not hard to see that there is a holomorphic map

$\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})\to\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)^\ast(\mathbb{C})$ .

The minor miracle is that this is actually a Zariski open embedding, and so defines a quasi-projective complex variety structure on $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)(\mathbb{C})$ . Moreover, by a hyperbolicity argument (again related to the unstated conditions on $(\mathbf{G},X)$ ) this has the desired property as in Baily–Borel’s theorem. $\blacklozenge$

Step 4: descent to reflex field

We now come to the most opaque part of the construction, the one that makes the arithmetic-geometry of Shimura varieties so complicated: the descent from a $\mathbb{C}$ -variety to a $\mathbf{E}$ -variety.

Remark: Often one thinks of Shimura varieties as varieties over $\mathbb{C}$ . From this perspective, the descent to $\mathbf{E}$ is not part of the definitional structure, but a choice: there could be several models over $\mathbf{E}$ . Which one do we choose? The one we will describe now is the so-called canonical model. We will see below why this name is justified. $\blacklozenge$

By quasi-projectivity it turns out (see [Milne4]) that giving such a descent is (essentially) equivalent to defining a (‘continuous’) action of the group $\mathrm{Aut}(\mathbb{C}/\mathbf{E})$ on $\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_\mathbb{C}$ .

The definition of this action is ‘done’ in two steps:

Step 4.A:

When $(\mathbf{G},X)$ is of a very simple type, namely toral type, i.e., $(\mathbf{G},X)=(\mathbf{T},\{\ast\})$ for a $\mathbb{Q}$ -torus $\mathbf{T}$ , one can define this action using class field theory.

Remark: Let me slightly expand on this. As $X=\{\ast\}$ is a point, $\mathrm{Sh}_\mathsf{L}(\mathbf{T},\{\ast\})$ is a finite disjoint union of copies of $\mathrm{Spec}(\mathbb{C})$ . This automatically has a unique model over $\overline{\mathbb{Q}}=\overline{\mathbf{E}}$ (something not guaranteed) by taking the corresponding disjoint union of copies of $\mathrm{Spec}(\overline{\mathbb{Q}})$ .

We then need to define an action of $\mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})$ on this $\overline{\mathbb{Q}}$ -model. Class field theory gives us a map

$\mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})\to (\mathbb{A}\otimes\mathbf{E})^\times$ .

As $\mu_h\colon \mathbb{G}_{m,\mathbb{C}}\to \mathbf{T}_\mathbb{C}$ is defined over $\mathbf{E}$ (by definition!) we get a map

$(\mathbb{A}\otimes\mathbf{E})^\times\xrightarrow{\mu_h} \mathbf{T}(\mathbb{A}\otimes \mathbf{E})\xrightarrow{N_{\mathbf{E}/\mathbb{Q}}} \mathbf{T}(\mathbb{A})$ ,

where this second map is the norm map for $\mathbf{T}$ . Combining these two maps gives us a map

$\mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})\to \mathbf{T}(\mathbb{A})$ ,

and the action on $\mathsf{Sh}_\mathsf{L}(\mathbf{T},\{\ast\})(\mathbb{C})=\mathbf{T}(\mathbb{Q})\backslash \mathbf{T}(\mathbb{A})/\mathsf{L}$ is now clear. $\blacklozenge$

Step 4.B:

We now bootstrap from Step 4.A. More precisely, we show that there are enough special points, i.e., points in the image of a map of the form

$\mathrm{Sh}_\mathsf{L}(\mathbf{T},\{\ast\})_\mathbb{C}\to\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)_\mathbb{C}$ ,

for some toral Shimura variety (see Proposition (prop:canonical) below for how such a map is defined). If you have enough such special points, it’s believable that one can uniquely specify an action of $\mathrm{Aut}(\mathbb{C}/\mathbf{E})$ using Step 4.A as input.

Remark: The above description of Step 4.B is an immense oversimplification. First, it’s not even clear what enough means. The reflex fields of these special points will (in general) be bigger than $\mathbf{E}$ , but one is still somehow hoping that you get enough juice out of the special points as you vary them (i.e., the interesection of their reflex fields is close to $\mathbf{E}$ ).

Secondly, this may help you determine what the $\mathrm{Aut}(\mathbb{C}/\mathbf{E})$ action must be, but it doesn’t help you necessarily prove it exists. Step 4.A forces how $\mathrm{Aut}(\mathbb{C}/\mathbf{E})$ acts on special points, and having enough such special points might by some ‘continuity argument’ force the action to be unique if it exists, but how do you extend the action beyond the special points?

It is perhaps telling that this last step was not completed until 1983 by Borovoi and Milne (see [Milne5]), nearly 15 years after the introduction of Shimura varieties. Moreover, the ultimate solution is still quite ‘opaque’–one does not ever really get an explicit description of the action of $\mathrm{Aut}(\mathbb{C}/\mathbf{E})$ which is (one of) the culprit(s) for the arithmetic mystery of general Shimura varieties. $\blacklozenge$

The output

Let us now try to explicitly describe what the output of the above procedure is: what actual structure do you get out of the theory of Shimura varieties.

The individual Shimura varieties

To begin with, let us state the obvious. For each Shimura datum $(\mathbf{G},X)$ and each level structure $\mathsf{K}$ one gets a smooth quasi-projective variety over the reflex field $\mathbf{E}=\mathbf{E}(\mathbf{G},X)$ .

The fact that these models are the right ones, thus justifying the name ‘canonical model’, is that they satisfy the following amazing functoriality property.

Proposition (prop:canonical)[Deligne]: Suppose that $f\colon (\mathbf{G}_1,X_1)\to (\mathbf{G}_2,X_2)$ is a morphism of Shimura data. Then, for any levels $\mathsf{K}_i\subseteq\mathbf{G}_1(\mathbb{A}_f)$ with $f(\mathsf{K}_1)\subseteq \mathsf{K}_2$ the map of sets

$\mathrm{Sh}_{\mathsf{K}_1}(\mathbf{G}_1,X_1)(\mathbb{C})\to \mathrm{Sh}_{\mathsf{K}_2}(\mathbf{G}_2,X_2)(\mathbb{C}),\quad \mathbf{G}_1(\mathbb{Q})(x,g)\mathsf{K}_1 \mapsto \mathbf{G}_2(\mathbb{Q})(f(x),f(g))\mathsf{K}_2$ ,

descends uniquely to a map of varieties over the compositum of the reflex fields:

$\mathrm{Sh}_{\mathsf{K}_1}(\mathbf{G}_1,X_1)_{\mathbf{E}_1\mathbf{E}_2}\to \mathrm{Sh}_{\mathsf{K}_2}(\mathbf{G}_2,X_2)_{\mathbf{E}_1\mathbf{E}_2}$ .

Remark: On the one hand, this functoriality is quite amazing as the set-theoretic map underlying this map of $\mathbf{E}$ -varieties is of an Archimedean-Hodge-theoretic flavor. So the fact that they admit arithmetic models is incredible. On the other hand, it’s not that surprising technically. Namely, it is easy to check by hand that this result holds for toral-type Shimura varieties. This then essentially concludes the proof as descending the map is the same as being equivariant for the action of $\mathrm{Aut}(\mathbb{C}/\mathbf{E}_1\mathbf{E}_2)$ and this action is determined on special points. $\blacksquare$

From the perspective of Expectation (exp:Shim-var), it’s clear what this map should do. Given a $\mathbb{Q}$ -motive $\omega$ with $\mathbf{G}_1$ -structure on $S$ , we get a $\mathbb{Q}$ -motive with $\mathbf{G}_2$ structure $f_\ast(\omega)$ via the rule:

$f_\ast(\omega)(\rho)=\omega(\rho\circ f)$ ,

i.e., if $\rho\colon \mathbf{G}_2\to \mathrm{GL}(V)$ is a representation of $\mathbf{G}_2$ , then $\rho\circ f$ is a representation of $\mathbf{G}_1$ and so it makes sense to apply $\omega$ to it. This is of type $X$ by our assumption that $f(X_1)\subseteq X_2$ , and assuming $f(\mathsf{K}_1)\subseteq \mathsf{K}_2$ it’s easy to see that an étale $\mathsf{K}_1$ -level structure on $\omega$ induces an étale $\mathsf{K}_2$ -level structure on $f_\ast(\omega)$ .

The Hecke action

The second, and in some sense equally important, output of our construction of Shimura varieties is the so-called Hecke action. This takes the form of the existence of two types of special maps between the Shimura varieties for $(\mathbf{G},X)$ at different levels.

The maps $[g]_\mathsf{K}$

For any element $g$ of $\mathbf{G}(\mathbb{A}_f)$ and level $\mathsf{K}\subseteq\mathbf{G}(\mathbb{A}_f)$ , one can produce an isomorphism

$[g]_{\mathsf{K}}\colon \mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)\xrightarrow{\sim}\mathrm{Sh}_{g^{-1}\mathsf{K}g}(\mathbf{G},X)$

which on $\mathbb{C}$ -points is given by

$[g]_{\mathsf{K}}\colon \mathbf{G}(\mathbb{Q})(x,g')\mathsf{K}\mapsto \mathbf{G}(\mathbb{Q})(x,g'g)g^{-1}\mathsf{K}g$ .

One again exploits the canonical model structure to show this map is defined over $\mathbf{E}$ .

From the perspective of Expectation (exp:Shim-var), the map $[g]_{\mathsf{K}}$ is the result of using $g$ to modify the étale $\mathsf{K}$ -level structure (to an étale $g^{-1}\mathsf{K}g$ -level structure).

The maps $\pi_{\mathsf{K},\mathsf{K}'}$

For any normal containment of levels $\mathsf{K}\unlhd\mathsf{K}'$ one builds a a projection map

$\pi_{\mathsf{K},\mathsf{K}'}\colon \mathrm{Sh}_\mathsf{K}(\mathbf{G},X)\to\mathrm{Sh}_{\mathsf{K}'}(\mathbf{G},X)$

which on $\mathbb{C}$ -points is given by

$\pi_{\mathsf{K},\mathsf{K}'}\colon \mathbf{G}(\mathbb{Q})(x,g)\mathsf{K}\mapsto \mathbf{G}(\mathbb{Q})(x,g)\mathsf{K}'$ .

and is a Galois cover with Galois group $\mathsf{K}'/\mathsf{K}$ (with a coset $g\mathsf{K}$ acting as $[g]_{\mathsf{K}}$ ).

Remark: The phrase ‘Galois cover’ often assumes that the source and target is connected. This is not the case here. So, what I really mean is that $\pi_{\mathsf{K},\mathsf{K}'}$ is a torsor for the constant group scheme associated to the finite group $\mathsf{K}'/\mathsf{K}$ . $\blacklozenge$

From the perspective of Expectation (exp:Shim-var), the map $\pi_{\mathsf{K},\mathsf{K}'}$ takes an étale $\mathsf{K}$ -level structure and applies the ‘blurrification’ obtained by taking the associated étale $\mathsf{K}'$ -level structure, which exactly forgets $\mathsf{K}'/\mathsf{K}$ -worth of information.

The action at infinite level

It is often useful to combine the information of the maps $[g]_\mathsf{K}$ and $\pi_{\mathsf{K},\mathsf{K}'}$ into one package. Namely, we can consider the $\mathbf{E}$ -scheme

$\displaystyle \mathrm{Sh}(\mathbf{G},X):=\varprojlim_{\mathsf{K}}\mathrm{Sh}_{\mathsf{K}}(\mathbf{G},X)$ ,

with the transition maps given by $\pi_{\mathsf{K},\mathsf{K}'}$ . As these transition maps are finite (and thus affine), this actually does exist as a scheme over $\mathbf{E}$ . Moreover, as we are limiting over all levels, one actually sees that each element $g$ of $\mathbf{G}(\mathbb{A}_f)$ gives a morphism of $\mathbf{E}$ -schemes

$[g]\colon \mathrm{Sh}(\mathbf{G},X)\to \mathrm{Sh}(\mathbf{G},X)$ .

This defines a continuous action of $\mathbf{G}(\mathbb{A}_f)$ on $\mathrm{Sh}(\mathbf{G},X)$ in the sense of [Milne6, §II.10].

Given Expectation (exp:Shim-var), one would expect that for $S$ a smooth quasi-compact $\mathbf{E}$ -variety that

$\mathrm{Sh}(\mathbf{G},X)(S)=\left\{\begin{matrix}\mathbb{Q}\text{-motives with }\mathbf{G}\text{-structure }\omega\text{ of type}\\ X\text{ and with a trivialization }(\omega_\ell)\xrightarrow{\sim}(\omega_\ell^\mathrm{triv}).\end{matrix}\right\}^{\simeq}$

From this perspective the map $[g]$ is just modifying this trivialization, and the projection maps

$\pi_\mathsf{K}\colon\mathrm{Sh}(\mathbf{G},X)\to\mathrm{Sh}_\mathsf{K}(\mathbf{G},X)$

are just sending such a trivialization to its class in $\underline{\mathrm{Isom}}((\omega_\ell),(\omega_\ell^\mathrm{triv}))/\mathsf{K}$ .

Hecke correspondences

One often hears of ‘Hecke correspondences’ for Shimura varieties, and so it might be helpful to explain how this facets into the theory. Namely, suppose that we have two different levels $\mathsf{L}$ and $\mathsf{L}'$ in $\mathbf{G}(\mathbb{A}_f)$ . Then, there is no direct way to relate them by the maps $[g]_\mathsf{K}$ and $\pi_{\mathsf{K},\mathsf{K}'}$ , but there is always a relate them via a correspondence. Namely, we obtain the following correspondence

from $\mathrm{Sh}_\mathsf{L}(\mathbf{G},X)$ to $\mathrm{Sh}_{\mathsf{L}'}(\mathbf{G},X)$ , where we have written $\mathsf{L}'':=\mathsf{L}\cap g\mathsf{L}'g^{-1}$ for simplicity. This is often called a Hecke correspondence.

Remark: The reason that Hecke correspondences are useful is because of their relationship with cohomology, which is of great importance as we will see in §3.2.1 below. Namely, taking $\mathsf{L}=\mathsf{L}'$ in the definition of the Hecke correspondence allows one to build (via standard theory) a morphism of cohomology groups

$H^i_\mathrm{\acute{e}t}(\mathrm{Sh}_{\mathsf{L}}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)\to H^i_\mathrm{\acute{e}t}(\mathrm{Sh}_{\mathsf{L}}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)$

compatible with $\mathrm{Gal}(\overline{\mathbf{E}}/\mathbf{E})$ -action.

In fact, one can understand this action in another useful way. Namely, the action of $\mathbf{G}(\mathbb{A}_f)$ action on $\mathrm{Sh}(\mathbf{G},X)$ defines an action of $\mathbf{G}(\mathbb{A}_f)$ on $H^i_\mathrm{\acute{e}t}(\mathrm{Sh}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)$ . Moreover, for any level $\mathsf{L}$ there is a natural identification

$H^i_\mathrm{\acute{e}t}(\mathrm{Sh}_{\mathsf{L}}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)=H^i_\mathrm{\acute{e}t}(\mathrm{Sh}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)^\mathsf{L}$ .

From standard representation theory of locally profinite group this endows the cohomology group $H^i_\mathrm{\acute{e}t}(\mathrm{Sh}_{\mathsf{L}}(\mathbf{G},X)_{\overline{\mathbf{E}}},\overline{\mathbb{Q}}_\ell)$ with an action of the Hecke algebra $\mathcal{H}(\mathbf{G}(\mathbb{A}_f),\mathsf{L})$ . As is well-known, this algebra is generated by indicator functions of the form $\mathbf{1}_{g\mathsf{L}g^{-1}}$ , and the action of this function on the cohomology group agrees with that coming from the Hecke correspondence above.

Of course, this all works for more general coefficients–so-called, automorphic local systems. $\blacklozenge$

References

[AchingerYoucis] https://arxiv.org/pdf/2410.20500

[AGHM] Andreatta, F., Goren, E., Howard, B. and Madapusi Pera, K., 2018. Faltings heights of abelian varieties with complex multiplication. Annals of Mathematics, 187(2), pp.391-531.

[BST] https://arxiv.org/pdf/2405.12392

[Baez] https://arxiv.org/pdf/2304.08737

[Broshi] Broshi, M., 2013. G-torsors over a Dedekind scheme. Journal of Pure and Applied Algebra, 217(1), pp.11-19.

[Conrad] https://math.stanford.edu/~conrad/papers/luminysga3.pdf

[CMSP] Carlson, J., Müller-Stach, S. and Peters, C., 2017. Period mappings and period domains. Cambridge University Press.

[Deligne1] https://www.numdam.org/item/SB_1970-1971__13__123_0.pdf

[Deligne2] https://publications.ias.edu/sites/default/files/34_VarietesdeShimura.pdf

[Deligne3] https://www.numdam.org/item/PMIHES_1971__40__5_0.pdf

[FujiwaraKato] Fujiwara, K. and Kato, F., 2006. Rigid geometry and applications. Moduli spaces and arithmetic geometry, Adv. Stud. Pure Math, 45, pp.327-386.

[GenestierNgo] https://www.math.uchicago.edu/~ngo/Shimura.pdf

[Hida] Hida, H., 2004. p-adic automorphic forms on Shimura varieties. New York: Springer.

[Hoermann] https://fhoermann.org/shimura2.pdf

[Kerr] https://www.math.wustl.edu/~matkerr/SV.pdf

[Kisin] Kisin, M., 2010. Integral models for Shimura varieties of abelian type. Journal of the American Mathematical Society, 23(4), pp

[Kottwitz1] Kottwitz, R.E., 1984. Shimura varieties and twisted orbital integrals. Mathematische Annalen, 269(3), pp.287-300.

[Lan] https://www.kwlan.org/articles/intro-sh-ex.pdf

[Madapusi] Madapusi Pera, K., 2015. The Tate conjecture for K3 surfaces in odd characteristic. Inventiones mathematicae, 201(2), pp.625-668.

[Milne1] https://www.jmilne.org/math/xnotes/svi.pdf

[Milne2] https://www.jmilne.org/math/articles/1994bP.pdf

[Milne3] https://www.jmilne.org/math/xnotes/MOT.pdf

[Milne4] https://www.jmilne.org/math/articles/DT.pdf

[Milne6] https://www.jmilne.org/math/articles/1990aT.pdf

[Milne7] https://www.jmilne.org/math/xnotes/svh.pdf

[Milne8] https://www.jmilne.org/math/xnotes/Montreal.pdf

[Moonen] https://www.math.ru.nl/~bmoonen/Papers/SMCfinal.pdf

[Morel] https://fhoermann.org/shimura2.pdf

[Rosen] Rosen, M., 1986. Abelian varieties over C. Arithmetic geometry, pp.79-101.

[Serre] https://www.numdam.org/item/SCC_1958-1959__4__A10_0.pdf

[Vasiu] Vasiu, A., 1999. Integral canonical models of Shimura varieties of preabelian type. Asian Journal of Mathematics, 3, pp.401-517.

[Yang] https://arxiv.org/pdf/2304.10751

A taster of rigid geometry (Pt I: the Tate perspective)

This is the first in a series of 5 posts whose goal is to briefly introduce rigid geometry with a focus on providing a big picture between the interactions between different perspectives of rigid geometry.

(more…)

Objects with no rational models

The goal of this post, which is just a bit of fun between more serious posts/projects, is to discuss some examples of algebro-geometric objects over $\overline{\mathbb{Q}}$ which have no models over smaller subfields and explain how moduli theory can help clarify their discovery in certain situations.

(more…)

A new paper draft

I have not been able to post of late as I’ve been quite busy working on several projects.

I wanted to make a post though discussing a new draft with my collaborator A. Bertoloni Meli that I’m quite excited about. In it we discuss a method for characterizing the local Langlands conjecture for certain groups $G$ as in Scholze’s paper [Sch]. Namely we show that for certain classes of groups an equation like that in the Scholze–Shin conjecture (see [Conjecture 7.1, SS]) is enough to characterize the local Langlands conjecture (for supercuspidal parameters) at least if one is willing to assume that other expected properties of the local Langlands conjecture hold.

The main original idea of this paper is the realization that while the Langlands–Kottwitz–Scholze method only deals with Hecke operators at integral level (e.g. see the introduction to [Sch]) that one can circumvent the difficult questions this raises (e.g. see [Question 7.5,SS]) if one is willing to not only consider the local Langlands conjecture for $G$ in isolation, but also the local Langlands conjecture for certain groups closely related to $G$ (so-called elliptic hyperendoscopic groups). Another nice byproduct of this approach is that while the Scholze–Shin conjecture is stated as a set of equations for all endoscopic triples for $G$ our paper shows that one needs only consider the trivial endoscopic situation (for elliptic hyperendoscopic groups of $G$ ).

This paper is closely related to the paper mentioned in this previous post where me and A. Bertoloni Meli discuss the proof of the Scholze–Shin conjecture for unramified unitary groups in the trivial endoscopic triple setting.

References

[Sch] Scholze, Peter. The Local Langlands Correspondence for GL_n over $p$ -adic fields, Invent. Math. 192 (2013), no. 3, 663–715.

[SS] Scholze, P. and Shin, S., 2013. On the cohomology of compact unitary group Shimura varieties at ramified split places. Journal of the American Mathematical Society, 26(1), pp.261-294.

Punctured disks and punctured curves and cohomology, oh my! (Part III: the affine curve case)

This is a continuation of this post.

(more…)

Original Source | Taken Source

(more…)

§3 How and why?

§3.1 How?

Archimedean-type methods

Special points

“Type theory”

§3.2 Why?

§3.2.1 Langlands

Other applications to algebraic geometry/number theory/harmonic analysis/differential geometry

A measuring stick for understanding of motives

§4 “Type theory”

Modular curves

Siegel type

PEL, Hodge, Abelian, and General type

PEL type

Hodge type

Abelian type

General type

§5 Integral canonical models

Setup

Answer 1: the Langlands–Rapoport conjecture

Answer 2: motivic expectation

Answer 3: an extension property

Known cases

§6 A toy example

Statement of the theorem

What is a scheme over anyways?

References

§0 motives and objects with -structure

§0.1 Motives

§0.1.1 Abelian varieties

§0.1.2 Archimedean Hodge theory

§0.2 Objects with -structure

§1 A dreamland: moduli of motives

§2 Harsh reality: the lifecycle of a Shimura variety

The construction, in steps

Step 1: real manifold

Step 2: complex manifold

Step 3: complex variety

Step 4: descent to reflex field

Step 4.A:

Step 4.B:

The output

The individual Shimura varieties

The Hecke action

The maps

The maps

The action at infinite level

Hecke correspondences

References

What is a scheme over $\mathbb{Z}_p$ anyways?

§0 motives and objects with $H$ -structure

§0.2 Objects with $H$ -structure

The maps $[g]_\mathsf{K}$

The maps $\pi_{\mathsf{K},\mathsf{K}'}$