| CARVIEW |
Minimum Spanning Trees /Shortest Path Algorithms GATE CS PYQ Quiz
Topic Wise PYQs Quiz on Minimum Spanning Trees / Shortest Path Algorithms GATE CS from 2025 to 2000
Question 1
Let G be a weighted graph with edge weights greater than one and G'be the graph constructed by squaring the weights of edges in G. Let T and T' be the minimum spanning trees of G and G', respectively, with total weights t and t'. Which of the following statements is TRUE?
T' = T with total weight t' = t2
T' = T with total weight t' < t2
T' != T but total weight t' = t2
None of the above
Question 2
Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices S and T. Which one will be reported by Dijkstra's shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex v is updated only when a strictly shorter path to v is discovered.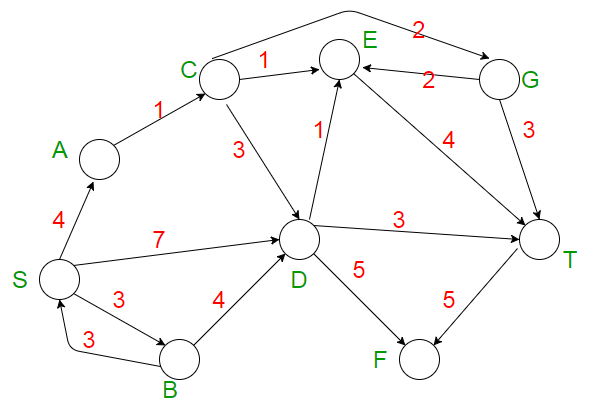
SDT
SBDT
SACDT
SACET
Question 3
Consider a graph G=(V, E), where V = { v1,v2,…,v100 }, E={ (vi, vj) ∣ 1≤ i < j ≤ 100} and weight of the edge (vi, vj) is ∣i–j∣. The weight of minimum spanning tree of G is ________.
99
100
98
101
Question 4
Given below are some algorithms, and some algorithm design paradigms.
List-I
A. Dijkstra’s Shortest Path
B. Floyd-Warshall algorithm to compute all pairs shortest path
C. Binary search on a sorted array
D. Backtracking search on a graph
List-II
1. Divide and Conquer
2. Dynamic Programming
3. Greedy design
4. Depth-first search
5. Breadth-first search
Match the above algorithms on the left to the corresponding design paradigm they follow Codes:
A B C D
(a) 1 3 1 5
(b) 3 3 1 5
(c) 3 2 1 4
(d) 3 2 1 5
a
b
c
d
Question 5
Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is
Θ(∣E∣ + ∣V∣)
Θ(∣E∣.∣V∣)
Θ(E∣ log ∣V∣)
Θ(∣V∣)
Question 6
Which of the following statement(s)is / are correct regarding Bellman-Ford shortest path algorithm?
P: Always finds a negative weighted cycle, if one exist s.
Q: Finds whether any negative weighted cycle is reachable
from the source.
P Only
Q Only
Both P and Q
Neither P nor Q
Question 7
Let G be a complete undirected graph on 4 vertices, having 6 edges with weights being 1, 2, 3, 4, 5, and 6. The maximum possible weight that a minimum weight spanning tree of G can have is.
6
7
8
9
Question 8
G = (V, E) is an undirected simple graph in which each edge has a distinct weight, and e is a particular edge of G. Which of the following statements about the minimum spanning trees (MSTs) of G is/are TRUE
I. If e is the lightest edge of some cycle in G,
then every MST of G includes e
II. If e is the heaviest edge of some cycle in G,
then every MST of G excludes e
I only
II only
both I and II
neither I nor II
Question 9
Consider the following graph:
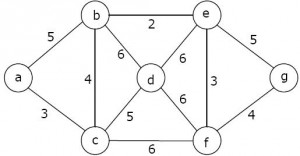
Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal's algorithm?
(b,e)(e,f)(a,c)(b,c)(f,g)(c,d)
(b,e)(e,f)(a,c)(f,g)(b,c)(c,d)
(b,e)(a,c)(e,f)(b,c)(f,g)(c,d)
(b,e)(e,f)(b,c)(a,c)(f,g)(c,d)
Question 10
The number of distinct minimum spanning trees for the weighted graph below is ____
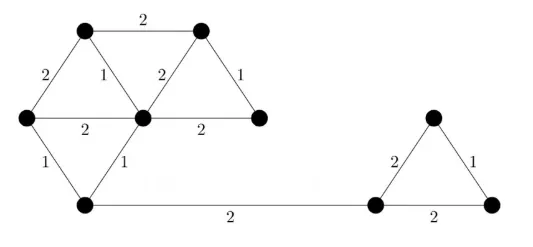
4
5
6
7
There are 29 questions to complete.





