| CARVIEW |
Dynamic Programming GATE CS PYQ Quiz
Topic Wise PYQs Quiz on Dynamic Programming GATE CS from 2025 to 2000
Question 1
Let A1, A2, A3, and A4 be four matrices of dimensions 10 x 5, 5 x 20, 20 x 10, and 10 x 5, respectively. The minimum number of scalar multiplications required to find the product A1A2A3A4 using the basic matrix multiplication method is
1500
2000
500
100
Question 2
Consider two strings A = "qpqrr" and B = "pqprqrp". Let x be the length of the longest common subsequence (not necessarily contiguous) between A and B and let y be the number of such longest common subsequences between A and B. Then x + 10y = ___.
33
23
43
34
Question 3
A sub-sequence of a given sequence is just the given sequence with some elements (possibly none or all) left out. We are given two sequences X[m] and Y[n] of lengths m and n respectively, with indexes of X and Y starting from 0. We wish to find the length of the longest common sub-sequence(LCS) of X[m] and Y[n] as l(m,n), where an incomplete recursive definition for the function l(i,j) to compute the length of The LCS of X[m] and Y[n] is given below:
l(i,j) = 0, if either i=0 or j=0
= expr1, if i,j > 0 and X[i-1] = Y[j-1]
= expr2, if i,j > 0 and X[i-1] != Y[j-1]
expr1 ≡ l(i-1, j) + 1
expr1 ≡ l(i, j-1)
expr2 ≡ max(l(i-1, j), l(i, j-1))
expr2 ≡ max(l(i-1,j-1),l(i,j))
Question 4
The Floyd-Warshall algorithm for all-pair shortest paths computation is based on:
Greedy paradigm.
Divide-and-Conquer paradigm.
Dynamic Programming paradigm.
neither Greedy nor Divide-and-Conquer nor Dynamic Programming paradigm.
Question 5
What is the weight of a minimum spanning tree of the following graph?
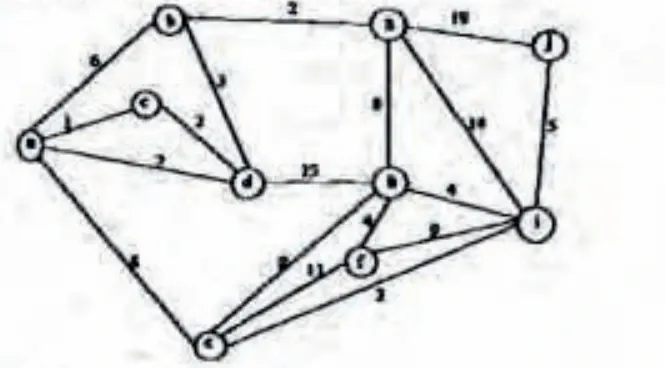
29
31
38
41
Question 6
An algorithm to find the length of the longest monotonically increasing sequence of numbers in an array A[0 :n-1] is given below.
Let Li denote the length of the longest monotonically increasing sequence starting at index i in the array

Which of the following statements is TRUE?
The algorithm uses dynamic programming paradigm
The algorithm has a linear complexity and uses branch and bound paradigm
The algorithm has a non-linear polynomial complexity and uses branch and bound paradigm
The algorithm uses divide and conquer paradigm.
Question 7
A sub-sequence of a given sequence is just the given sequence with some elements (possibly none or all) left out. We are given two sequences X [m] and Y [n] of lengths m and n, respectively, with indexes of X and Y starting from 0.
Consider the data given in the previous question. The values of l(i, j) could be obtained by dynamic programming based on the correct recursive definition of l(i, j) of the form given above, using an array L[M, N], where M = m+1 and N =n+1, such that L[i, j] = l(i, j).
Which one of the following statements would be TRUE regarding the dynamic programming solution for the recursive definition of l(i, j)?
All elements L should be initialized to 0 for the values of l(i,j) to be properly computed
The values of l(i,j) may be computed in a row major order or column major order of L(M,N)
The values of l(i,j) cannot be computed in either row major order or column major order of L(M,N)
L[p,q] needs to be computed before L[r,s] if either p < r or q < s.
Question 8
The subset-sum problem is defined as follows. Given a set of n positive integers, S = {a1 ,a2 ,a3 ,...,an} and positive integer W, is there a subset of S whose elements sum to W? A dynamic program for solving this problem uses a 2-dimensional Boolean array X, with n rows and W+1 columns. X[i, j], 1 <= i <= n, 0 <= j <= W, is TRUE if and only if there is a subset of {a1 ,a2 ,...,ai} whose elements sum to j. Which of the following is valid for 2 <= i <= n and ai <= j <= W?
X[i, j] = X[i - 1, j] V X[i, j -ai]
X[i, j] = X[i - 1, j] V X[i - 1, j - ai]
X[i, j] = X[i - 1, j] V X[i, j - ai]
X[i, j] = X[i - 1, j] V X[i -1, j - ai]
Question 9
The subset-sum problem is defined as follows. Given a set of n positive integers, S = {a1 ,a2 ,a3 ,...,an} and positive integer W, is there a subset of S whose elements sum to W? A dynamic program for solving this problem uses a 2-dimensional Boolean array X, with n rows and W+1 columns. X[i, j],1 <= i <= n, 0 <= j <= W, is TRUE if and only if there is a subset of {a1 ,a2 ,...,ai} whose elements sum to j. Which of the following is valid for 2 <= i <= n and ai <= j <= W? Which entry of the array X, if TRUE, implies that there is a subset whose elements sum to W?
X[1, W]
X[n, 0]
X[n, W]
X[n-1, n]
Question 10
The subset-sum problem is defined as follows. Given a set of n positive integers, S = {a1 ,a2 ,a3 ,...,an} and positive integer W, is there a subset of S whose elements sum to W? A dynamic program for solving this problem uses a 2-dimensional Boolean array X, with n rows and W+1 columns. X[i, j],1 <= i <= n, 0 <= j <= W, is TRUE if and only if there is a subset of {a1 ,a2 ,...,ai} whose elements sum to j. Which of the following is valid for 2 <= i <= n and ai <= j <= W?
X[i, j] = X[i - 1, j] V X[i, j -ai]
X[i, j] = X[i - 1, j] V X[i - 1, j - ai]
X[i, j] = X[i - 1, j] V X[i, j - ai]
X[i, j] = X[i - 1, j] V X[i -1, j - ai]
There are 11 questions to complete.





