Conditional Probability and Bayes Theorem for GATE

Consider Guwahati (G) and Delhi (D) whose temperatures can be classified as high (H), medium (M) and low (L). Let P(H_G) denote the probability that Guwahati has high temperature. Similarly, P(M_G) and P(L_G) denotes the probability of Guwahati having medium and low temperatures respectively. Similarly, we use P(H_D), P(M_D) and P(L_D) for Delhi.

The following table gives the conditional probabilities for Delhi’s temperature given Guwahati’s temperature.

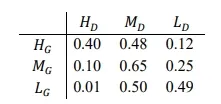
Consider the first row in the table above. The first entry denotes that if Guwahati has high temperature (H_G) then the probability of Delhi also having a high temperature (H_D) is 0.40; i.e., P(H_D ∣ H_G) = 0.40. Similarly, the next two entries are P(M_D ∣ H_G) = 0.48 and P(L_D ∣ H_G) = 0.12. Similarly for the other rows.

If it is known that P(H_G) = 0.2, P(M_G) = 0.5, and P(L_G) = 0.3, then the probability (correct to two decimal places) that Guwahati has high temperature given that Delhi has high temperature is _______ .


Note -This was Numerical Type question.

Consider the joint probability density function of the random variables X and Y

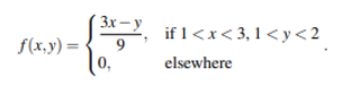
The conditional distribution P(Y/X = x) is 




 

Given the following Bayesian Network consisting of four Bernoulli random variables and the associated conditional probability tables:

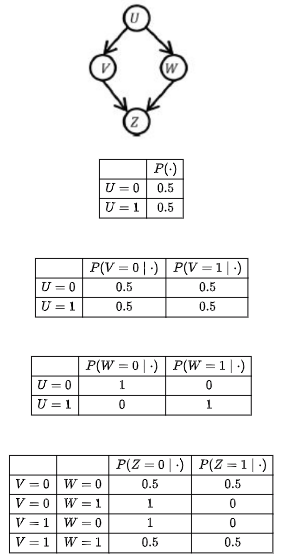
The value of P(U = 1, V = 1, W = 1, Z = 1) = _______.(rounded off to three decimal places).

In a scenario where two events A and B are independent, which statement is true regarding their conditional probabilities?

In a situation where the probability of event A is 0.3 and the probability of event B is 0.4, and they are independent, what is P(A ∩ B)?

In a group of 100 students, 60 play cricket, 50 play football, and 30 play both. If a student is selected at random, what is the probability that the student plays cricket given that the student plays football?

In a class, 60% of the students are girls, and 70% of the students like math. If 80% of the girls like math, what is the probability that a randomly selected math-loving student is a girl?

Given the following Bayesian Network consisting of four Bernoulli random variables and the associated conditional probability tables:

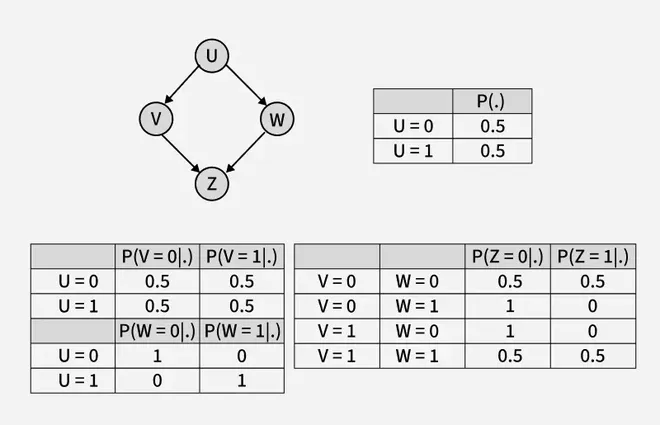
The value of 𝑃(𝑈 = 1, 𝑉 = 1, 𝑊 = 1,𝑍 = 1) = ______ (rounded off to three decimal places).

A dice is thrown two times and the sum of the scores appearing on the dice is observed to be a multiple of 4. Then the conditional probability that the score 4 has appeared at least once is:

In a binary transmission channel, a 1 is transmitted with probability 0.8 and a 0 with probability 0.2. The conditional probability of receiving a 1 given that a 1 was sent is 0.95, the conditional probability of receiving a 0 when a 0 was sent is 0.99. The probability that a 1 was sent when receiving a 1 is _______.